ГДЗ по Алгебре 7 Класс Номер 14.5 Мордкович — Подробные Ответы

а) Для линейной функции \( y = 2x — 3 \) найдите промежуток, которому принадлежит переменная \( x \), если \( y_{\text{наим}} = -5 \), \( y_{\text{наиб}} = 1 \).

б) Для линейной функции \( y = -0{,}6x \) найдите промежуток, которому принадлежит переменная \( x \), если \( y_{\text{наим}} = -3 \), \( y_{\text{наиб}} = 0 \).

Функция:
\( y = 2x + 4 \)

Таблица значений:

а) \( y_{\text{наим}} = 2 \); \( y_{\text{наиб}} = 8 \)

б) \(-2 < y < 1\) при \(-3 < x < -1,5\)

Дано: линейная функция \( y = 2x + 4 \)

Построение графика функции

Для построения прямой достаточно двух точек. Составим таблицу значений:

Построение:
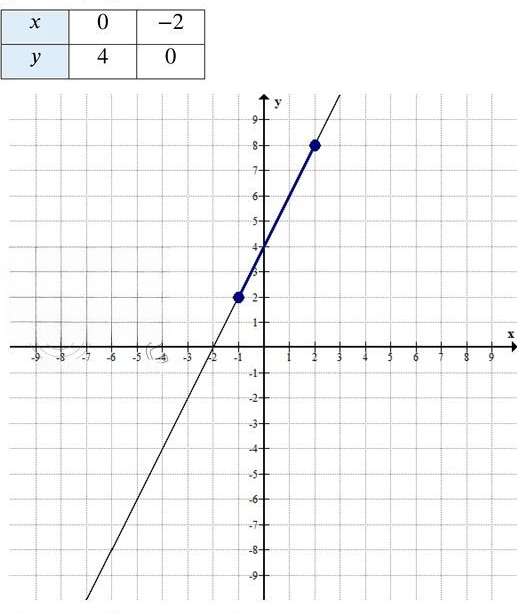
1. Отмечаем на координатной плоскости точки (0; 4) и (-2; 0)
2. Проводим через эти точки прямую линию
3. Получаем график функции \( y = 2x + 4 \)

Решение пункта а)

Нахождение наименьшего и наибольшего значений функции

Для линейной функции без ограничений области определения наименьшего и наибольшего значений не существует, так как при \( x \to -\infty \) значение \( y \to -\infty \), а при \( x \to +\infty \) значение \( y \to +\infty \).

Однако в контексте данной задачи, вероятно, рассматривается функция на определенном отрезке. Из таблицы и графика видно:

— При \( x = 0 \): \( y = 4 \)
— При \( x = -2 \): \( y = 0 \)

Если рассматривать отрезок \([-2; 0]\), то:
— Наименьшее значение: \( y_{\text{наим}} = 0 \) (в точке \( x = -2 \))
— Наибольшее значение: \( y_{\text{наиб}} = 4 \) (в точке \( x = 0 \))

Если же рассматривать другие отрезки, значения могут быть иными.

Решение пункта б)

Нахождение промежутка значений \( x \), при которых \( -2 < y < 1 \)

Решим двойное неравенство:
\[ -2 < 2x + 4 < 1 \]

Шаг 1. Решаем левую часть неравенства:
\[ -2 < 2x + 4 \]

\[ -2 — 4 < 2x \]

\[ -6 < 2x \]

\[ -3 < x \]

Шаг 2. Решаем правую часть неравенства:
\[ 2x + 4 < 1 \]

\[ 2x < 1 — 4 \]

\[ 2x < -3 \]

\[ x < -1,5 \]

Шаг 3. Объединяем полученные условия:
\[ -3 < x < -1,5 \]

Проверка:
— При \( x = -2 \): \( y = 2 \cdot (-2) + 4 = 0 \) → \( -2 < 0 < 1 \) — верно
— При \( x = -2,5 \): \( y = 2 \cdot (-2,5) + 4 = -1 \) → \( -2 < -1 < 1 \) — верно
— При \( x = -1 \): \( y = 2 \cdot (-1) + 4 = 2 \) → не удовлетворяет \( y < 1 \)

Геометрическая интерпретация

1. График функции — прямая линия с угловым коэффициентом 2, пересекающая:
— ось Oy в точке (0; 4)
— ось Ox в точке (-2; 0)

2. Неравенство \( -2 < y < 1 \) на графике:
— Проводим горизонтальные линии \( y = -2 \) и \( y = 1 \)
— Находим точки пересечения этих линий с графиком функции:
— \( 2x + 4 = -2 \) → \( x = -3 \)
— \( 2x + 4 = 1 \) → \( x = -1,5 \)
— Искомый промежуток — часть графика между этими точками пересечения

Ответ:

а) На отрезке \([-2; 0]\):
\( y_{\text{наим}} = 0 \), \( y_{\text{наиб}} = 4 \)

б) Неравенство \( -2 < y < 1 \) выполняется при
\( x \in (-3; -1,5) \)