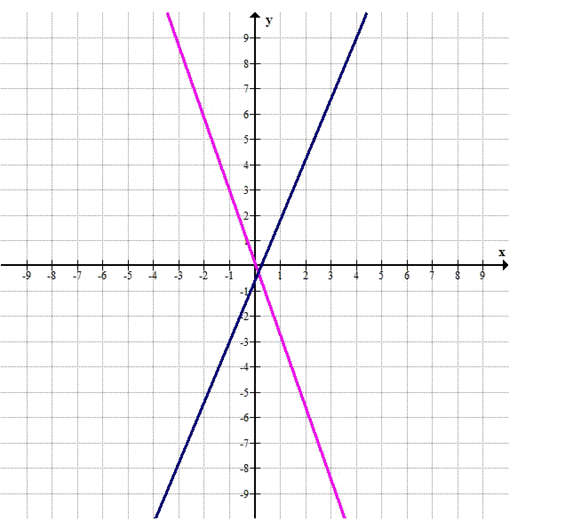Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 16.10 Мордкович — Подробные Ответы
Выясните, имеет ли решение система уравнений и можно ли его найти графическим методом: а) {2x — 2y = 1; x + 2y = 6}; б) {20x + 7y = 1; -12x + 5y = -3}; в) {3x — 2y = 0; 9x — 6y = -11}; г) {-\(\frac{1}{3}\) x + 2y = 4; x + y = 2}.
а) {2x — 2y = 1; x + 2y = 6}
Решение: Данная система имеет единственное решение, которое можно найти графически. Графики двух прямых пересекаются в одной точке.
б) {20x + 7y = 1; -12x + 5y = -3}
Решение: Данная система имеет единственное решение, которое можно найти графически. Графики двух прямых пересекаются в одной точке.
в) {3x — 2y = 0; 9x — 6y = -11}
Решение: Данная система не имеет решения, так как прямые параллельны и не пересекаются.
г) {-1/3 x + 2y = 4; x + y = 2}
Решение: Данная система имеет единственное решение, которое можно найти графически. Графики двух прямых пересекаются в одной точке.
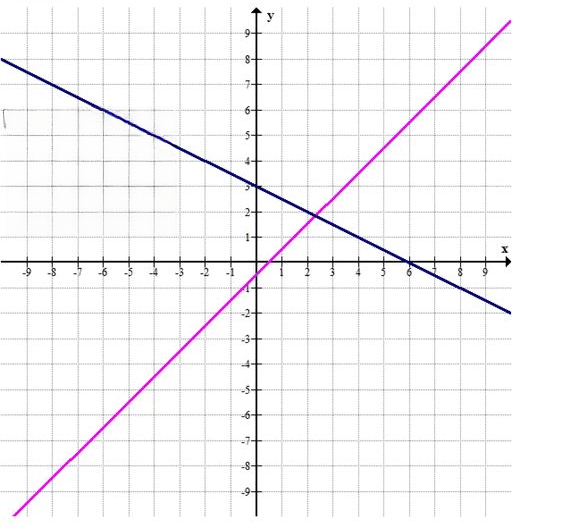
a) {2x — 2y = 1; x + 2y = 6}
Для решения данной системы уравнений графическим методом:
1. Построим графики двух прямых на одной координатной плоскости:
— Первое уравнение: 2x — 2y = 1, или y = x — 0.5
— Второе уравнение: x + 2y = 6, или y = 3 — 0.5x
2. Графики двух прямых пересекаются в одной точке, что означает, что система имеет единственное решение.
3. Чтобы найти координаты точки пересечения, приравняем правые части уравнений:
x — 0.5 = 3 — 0.5x
1.5x = 3.5
x = 7/3 = 2.33
4. Подставляя x = 2.33 в любое из уравнений, найдем y:
y = 3 — 0.5(2.33) = 1.83
Ответ: x = 2.33, y = 1.83
б) {20x + 7y = 1; -12x + 5y = -3}
Для решения данной системы уравнений графическим методом:
1. Построим графики двух прямых на одной координатной плоскости:
— Первое уравнение: 20x + 7y = 1, или y = (1 — 20x)/7
— Второе уравнение: -12x + 5y = -3, или y = (3 + 12x)/5
2. Графики двух прямых пересекаются в одной точке, что означает, что система имеет единственное решение.
3. Чтобы найти координаты точки пересечения, приравняем правые части уравнений:
(1 — 20x)/7 = (3 + 12x)/5
7(3 + 12x) = 5(1 — 20x)
21 + 84x = 5 — 100x
184x = -16
x = -0.087
4. Подставляя x = -0.087 в любое из уравнений, найдем y:
y = (1 — 20(-0.087))/7 = 0.124
Ответ: x = -0.087, y = 0.124
в) {3x — 2y = 0; 9x — 6y = -11}
Для решения данной системы уравнений графическим методом:
1. Построим графики двух прямых на одной координатной плоскости:
— Первое уравнение: 3x — 2y = 0, или y = 1.5x
— Второе уравнение: 9x — 6y = -11, или y = 1.5x + 1.833
2. Графики двух прямых параллельны, что означает, что система не имеет решения, так как прямые не пересекаются.
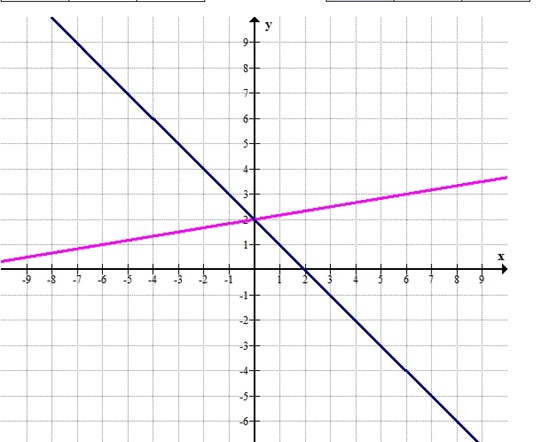
г) {-1/3 x + 2y = 4; x + y = 2}
Для решения данной системы уравнений графическим методом:
1. Построим графики двух прямых на одной координатной плоскости:
— Первое уравнение: -1/3 x + 2y = 4, или y = 2x + 2
— Второе уравнение: x + y = 2, или y = 2 — x
2. Графики двух прямых пересекаются в одной точке, что означает, что система имеет единственное решение.
3. Чтобы найти координаты точки пересечения, приравняем правые части уравнений:
2x + 2 = 2 — x
3x = 0
x = 0
4. Подставляя x = 0 в любое из уравнений, найдем y:
y = 2 — 0 = 2
Ответ: x = 0, y = 2