ГДЗ по Алгебре 7 Класс Номер 16.9 Мордкович — Подробные Ответы

Решите систему уравнений графическим методом. а) {x — 2y = 7; 3x + 2y = 5}; б) {2x + y = 1; 2x + y = 3}; в) {y = \(\frac{2}{5}\) x — 1; 4x — 10y = 10}; г) {x + y = -2; 2x — y = -4}; д) {y = -\(\frac{1}{3}\) x + 2; x + 3y = 3}; е) {x — 3y = 2; 2x — 6y = 4}.

а)
\[
\begin{cases}
x — 2y = 7 \\
3x + 2y = 5
\end{cases}
\]

— \(y = \frac{x — 7}{2}\)
— \(y = \frac{5 — 3x}{2}\)
Точка пересечения: (3, -2)

б)
\[
\begin{cases}
2x + y = 1 \\
2x + y = 3
\end{cases}
\]

— \(y = 1 — 2x\)
— \(y = 3 — 2x\)
Решений нет: Параллельные прямые.

в)
\[
\begin{cases}
y = \frac{2}{5} x — 1 \\
4x — 10y = 10
\end{cases}
\]

— Оба уравнения задают одну и ту же прямую.
Бесконечно много решений.

г)
\[
\begin{cases}
x + y = -2 \\
2x — y = -4
\end{cases}
\]

— \(y = -x — 2\)
— \(y = 2x + 4\)
Точка пересечения: (-2, 0)

д)
\[
\begin{cases}
y = -\frac{1}{3} x + 2 \\
x + 3y = 3
\end{cases}
\]

— \(y = -\frac{1}{3}x + 1\)
Решений нет: Параллельные прямые.

е)
\[
\begin{cases}
x — 3y = 2 \\
2x — 6y = 4
\end{cases}
\]

Бесконечно много решений.

Условие: Решите систему уравнений графическим методом.

а) \(\begin{cases} x — 2y = 7 \\ 3x + 2y = 5 \end{cases}\)

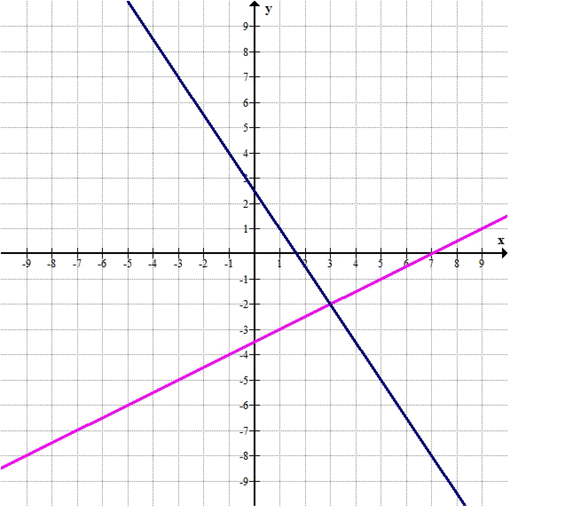
Решение: Выразим \(y\) из обоих уравнений: \(y = \frac{x — 7}{2}\) и \(y = \frac{5 — 3x}{2}\).

Построим графики этих функций и найдем точку пересечения.

Точка пересечения графиков — (3, -2). (3, -2)

б) \(\begin{cases} 2x + y = 1 \\ 2x + y = 3 \end{cases}\)

Решение:

Выразим \(y\) из обоих уравнений: \(y = 1 — 2x\) и \(y = 3 — 2x\).

Построим графики этих функций и заметим, что они параллельны.

Параллельные прямые не пересекаются. Решений нет.

в) \(\begin{cases} y = \frac{2}{5} x — 1 \\ 4x — 10y = 10 \end{cases}\)

Решение:

Выразим \(y\) из второго уравнения: \(10y = 4x — 10\), \(y = \frac{2}{5}x — 1\).

Оба уравнения задают одну и ту же прямую.

Прямые совпадают, значит, система имеет бесконечно много решений.

Бесконечно много решений.

г) \(\begin{cases} x + y = -2 \\ 2x — y = -4 \end{cases}\)

Решение:

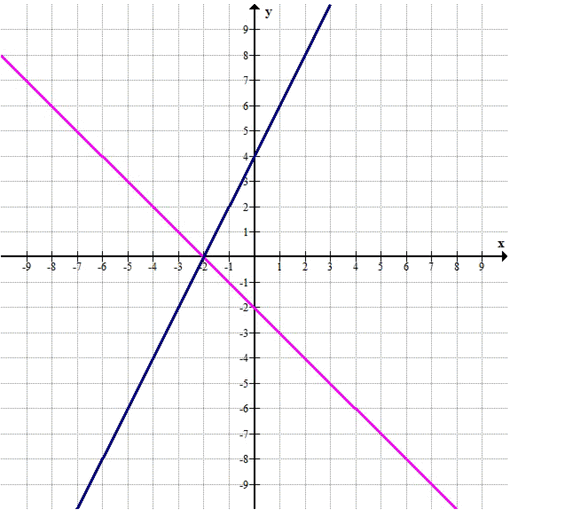
Выразим \(y\) из обоих уравнений: \(y = -x — 2\) и \(y = 2x + 4\).

Построим графики этих функций и найдем точку пересечения.

Точка пересечения графиков — (-2, 0). (-2, 0)

д) \(\begin{cases} y = -\frac{1}{3} x + 2 \\ x + 3y = 3 \end{cases}\)

Решение:

Выразим \(y\) из второго уравнения: \(3y = -x + 3\), \(y = -\frac{1}{3}x + 1\).

Построим графики этих функций и заметим, что они параллельны. Параллельные прямые не пересекаются.

Решений нет.

е) \(\begin{cases} x — 3y = 2 \\ 2x — 6y = 4 \end{cases}\)

Решение:

Выразим \(x\) из первого уравнения: \(x = 3y + 2\).

Выразим \(x\) из второго уравнения: \(2x = 6y + 4\), \(x = 3y + 2\).

Оба уравнения задают одну и ту же прямую. Бесконечно много решений.