ГДЗ по Алгебре 7 Класс Номер 20.13 Мордкович — Подробные Ответы

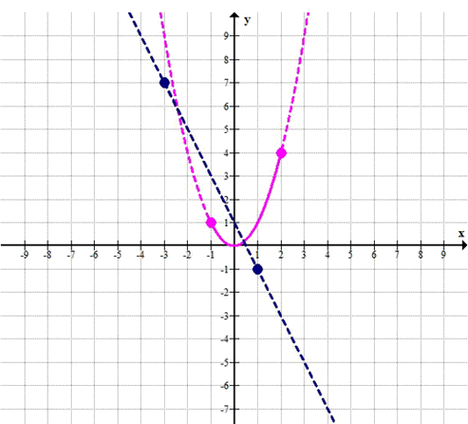
а) Пусть С — наибольшее значение функции \( y = x^2 \) на отрезке [—1; 2], a D — наименьшее значение функции у = —2x + 1 на отрезке [—3; 1]. Что больше — С или D? Сделайте графическую иллюстрацию. б) Пусть М — наибольшее значение функции \( y =- x^2 \) на отрезке [-2; 1], а N — наименьшее значение функции у = х + 1 на отрезке [—2; 2]. Что больше — М или N? Сделайте графическую иллюстрацию.

а)

\( y = x^2 \)

\( [-1; 2] \)

\( y(-1) = (-1)^2 = 1 \)

\( y(2) = 2^2 = 4 \)

\( C = 4 \)

\( y = -2x + 1 \)

\( [-3; 1] \)

\( y(-3) = -2(-3) + 1 = 6 + 1 = 7 \)

\( y(1) = -2(1) + 1 = -2 + 1 = -1 \)

\( D = -1 \)

\( C > D \)

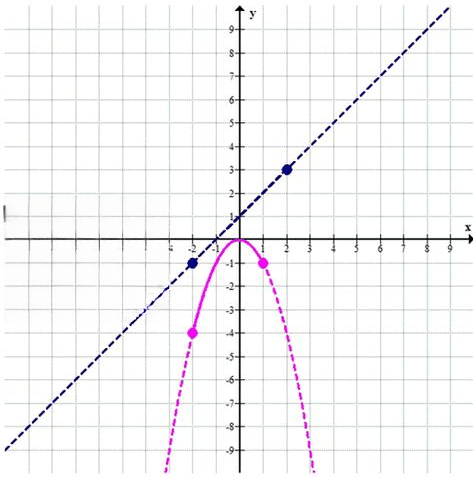
б)

\( y = -x^2 \)

\( [-2; 1] \)

\( y(-2) = -(-2)^2 = -4 \)

\( y(0) = -0^2 = 0 \)

\( y(1) = -1^2 = -1 \)

\( M = 0 \)

\( y = x + 1 \)

\( [-2; 2] \)

\( y(-2) = -2 + 1 = -1 \)

\( y(2) = 2 + 1 = 3 \)

\( N = -1 \)

\( M > N \)

Условие: Сравнить наибольшее значение функции \(y = x^2\)
на \([-1; 2]\)
и наименьшее значение функции \(y = -2x + 1\)
на \([-3; 1]\), а также наибольшее значение функции \(y = -x^2\)
на \([-2; 1]\)
и наименьшее значение функции \(y = x + 1\)
на \([-2; 2]\).

Решение:

а)

\(y = x^2\)
на \([-1; 2]\)

\(y(-1) = (-1)^2 = 1\)
— значение в точке -1
\(y(2) = (2)^2 = 4\)
— значение в точке 2
\(C = 4\)
— наибольшее значение

\(y = -2x + 1\)
на \([-3; 1]\)

\(y(-3) = -2(-3) + 1 = 7\)
— значение в точке -3
\(y(1) = -2(1) + 1 = -1\)
— значение в точке 1
\(D = -1\)
— наименьшее значение

\(C > D\)
— сравнение

б)

\(y = -x^2\)
на \([-2; 1]\)

\(y(-2) = -(-2)^2 = -4\)
— значение в точке -2
\(y(1) = -(1)^2 = -1\)
— значение в точке 1
\(y(0) = -(0)^2 = 0\)
— значение в точке 0
\(M = 0\)
— наибольшее значение

\(y = x + 1\)
на \([-2; 2]\)

\(y(-2) = -2 + 1 = -1\)
— значение в точке -2
\(y(2) = 2 + 1 = 3\)
— значение в точке 2
\(N = -1\)
— наименьшее значение

\(M > N\)
— сравнение

а) C > D;

б) M > N