Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 20.14 Мордкович — Подробные Ответы
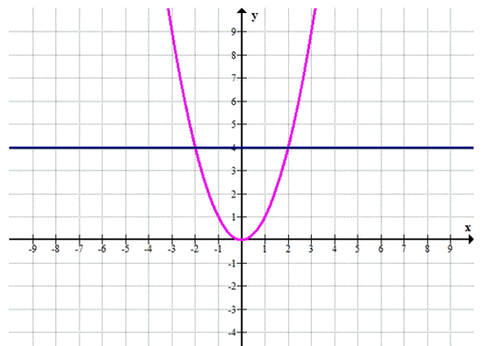
Найдите точки пересечения параболы \(у = х^2\) и данной прямой: а) y = 4; б) y = -1; в) y = 2; г) y = 1; д) y = -2; е) y = 0.
Условие: Найти точки пересечения параболы \(y = x^2\)
и прямых: \(y = 4\), \(y = -1\), \(y = 2\), \(y = 1\), \(y = -2\), \(y = 0\).
Решение:
а)
\(y = 4\)
\(x^2 = 4\)
— приравниваем
\(x = \pm 2\)
— извлекаем корень
Точки пересечения: \((-2; 4)\), \((2; 4)\)
б)
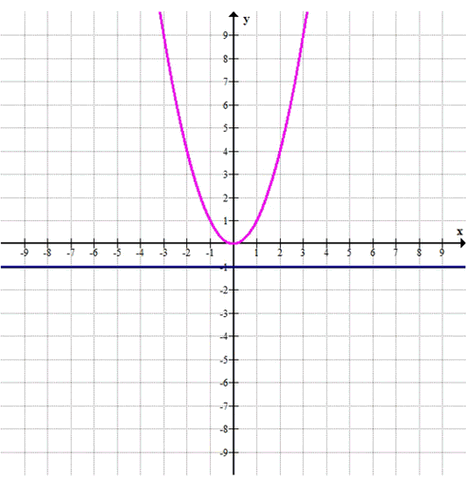
\(y = -1\)
\(x^2 = -1\)
— приравниваем
Нет решений, т.к. \(x^2 \ge 0\)
в)
\(y = 2\)
\(x^2 = 2\)
— приравниваем
\(x = \pm \sqrt{2}\)
— извлекаем корень
Точки пересечения: \((-\sqrt{2}; 2)\), \((\sqrt{2}; 2)\)
г)
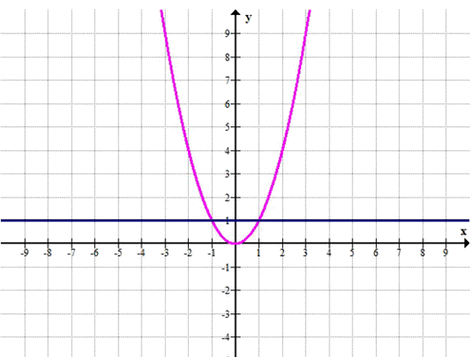
\(y = 1\)
\(x^2 = 1\)
— приравниваем
\(x = \pm 1\)
— извлекаем корень
Точки пересечения: \((-1; 1)\), \((1; 1)\)
д)
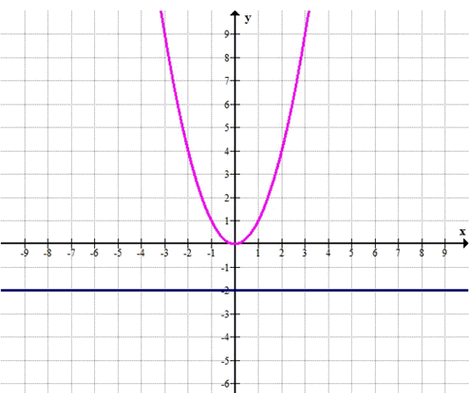
\(y = -2\)
\(x^2 = -2\)
— приравниваем
Нет решений, т.к. \(x^2 \ge 0\)
е)
\(y = 0\)
\(x^2 = 0\)
— приравниваем
\(x = 0\)
— извлекаем корень
Точка пересечения: \((0; 0)\)
а)
\((-2; 4)\), \((2; 4)\)
б) Нет пересечений
в)
\((-\sqrt{2}; 2)\), \((\sqrt{2}; 2)\)
г)
\((-1; 1)\), \((1; 1)\)
д) Нет пересечений
е)
\((0; 0)\)
Условие
Найти точки пересечения параболы \( y = x^2 \) с прямыми:
— \( y = 4 \)
— \( y = -1 \)
— \( y = 2 \)
— \( y = 1 \)
— \( y = -2 \)
— \( y = 0 \)
Решение
а) Прямая \( y = 4 \)
1. Приравниваем уравнения:
\[
x^2 = 4
\]
2. Извлекаем корень:
\[
x = \pm 2
\]
3. Точки пересечения:
\[
(-2, 4) \quad \text{и} \quad (2, 4)
\]
б) Прямая \( y = -1 \)
1. Приравниваем уравнения:
\[
x^2 = -1
\]
2. Анализируем решение:
— Нет действительных решений, так как \( x^2 \geq 0 \).
— Это означает, что парабола не пересекает прямую \( y = -1 \).
3. Результат:
\[
\text{Нет пересечений}
\]
в) Прямая \( y = 2 \)
1. Приравниваем уравнения:
\[
x^2 = 2
\]
2. Извлекаем корень:
\[
x = \pm \sqrt{2}
\]
3. Точки пересечения:
\[
(-\sqrt{2}, 2) \quad \text{и} \quad (\sqrt{2}, 2)
\]
г) Прямая \( y = 1 \)
1. Приравниваем уравнения:
\[
x^2 = 1
\]
2. Извлекаем корень:
\[
x = \pm 1
\]
3. Точки пересечения:
\[
(-1, 1) \quad \text{и} \quad (1, 1)
\]
д) Прямая \( y = -2 \)
1. Приравниваем уравнения:
\[
x^2 = -2
\]
2. Анализируем решение:
— Нет действительных решений, так как \( x^2 \geq 0 \).
— Это означает, что парабола не пересекает прямую \( y = -2 \).
3. Результат:
\[
\text{Нет пересечений}
\]
е) Прямая \( y = 0 \)
1. Приравниваем уравнения:
\[
x^2 = 0
\]
2. Извлекаем корень:
\[
x = 0
\]
3. Точка пересечения:
\[
(0, 0)
\]
Итоги
— а) Точки пересечения: \((-2, 4)\), \((2, 4)\)
— б) Нет пересечений
— в) Точки пересечения: \((-\sqrt{2}, 2)\), \((\sqrt{2}, 2)\)
— г) Точки пересечения: \((-1, 1)\), \((1, 1)\)
— д) Нет пересечений
— е) Точка пересечения: \((0, 0)\)
Заключение
Таким образом, мы нашли все точки пересечения параболы \( y = x^2 \) с заданными прямыми. Некоторые линии не пересекают параболу, что связано с тем, что они находятся ниже оси \( x \) и не могут иметь действительных решений.