Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 20.6 Мордкович — Подробные Ответы
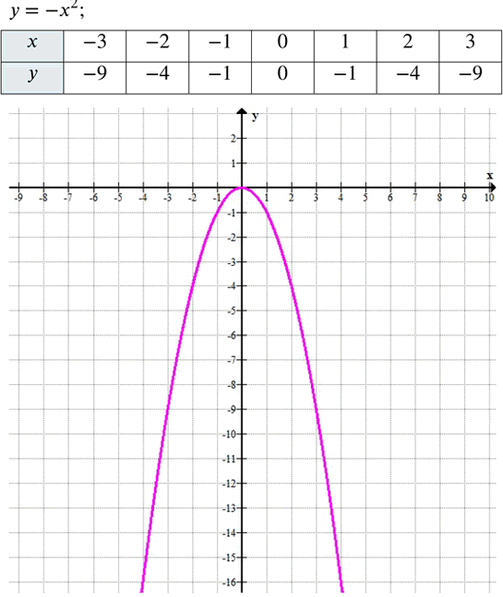
Постройте график функции \(у = — х^2\). С помощью графика найдите: а) значения функции при х = — 2, х = 2; б) значения аргумента, которым соответствует у = -4; в) значения х, если y < —4, y > —4; г) значения у, если —4 < х < 0.
a) Если x = -2, то y = -4; если x = 2, то y = -4.
б) Значения аргумента, которым соответствует y = -4, это x = -2 и x = 2.
в) Если y < -4, то x ∈ (-∞; -2) ∪ (2; +∞).
Если y > -4, то x ∈ (-2; 2).
г) Если -4 < x < 0, то y ∈ (-16; 0).
a) Если x = -2, то y = -4; если x = 2, то y = -4.
Это видно из таблицы значений функции \(у = — х^2\), представленной в условии задачи. Когда x = -2, y = -4, а когда x = 2, y также равно -4.
б) Значения аргумента, которым соответствует y = -4, это x = -2 и x = 2.
Из графика функции y = \(у = — х^2\) видно, что парабола пересекает горизонтальную линию y = -4 в двух точках: при x = -2 и x = 2.
в) Если y < -4, то x ∈ (-∞; -2) ∪ (2; +∞).
Если y > -4, то x ∈ (-2; 2).
Это следует из того, что парабола \(у = — х^2\) открывается вниз, и значения y < -4 соответствуют значениям x, лежащим вне интервала (-2; 2). А значения y > -4 соответствуют значениям x, принадлежащим интервалу (-2; 2).
г) Если -4 < x < 0, то y ∈ (-16; 0).
Из графика видно, что на промежутке -4 < x < 0 парабола \(у = — х^2\) принимает значения от -16 до 0.