Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 21.5 Мордкович — Подробные Ответы
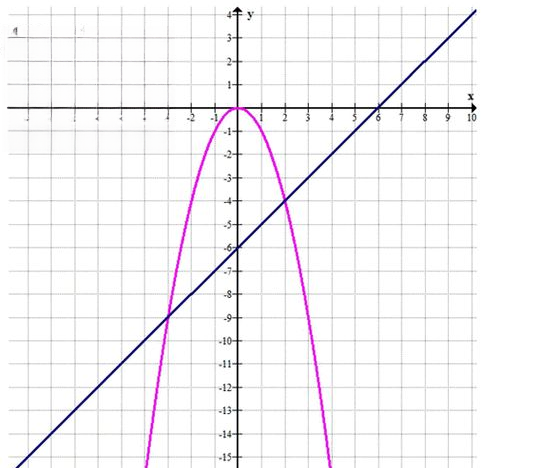
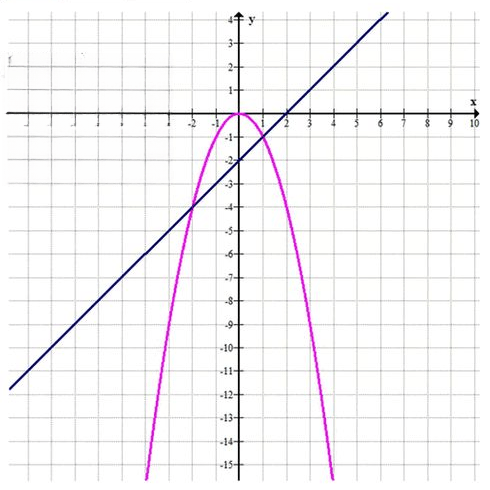
а) На графике функции \(у = —х^2\) найдите точку, ордината которой на б меньше абсциссы. б) На графике функции \(у = —х^2\) найдите точку, абсцисса которой на 2 больше ординаты.
а)
\( y = -x^2 \)
\( y = x — 6 \)
\( -x^2 = x — 6 \)
\( x^2 + x — 6 = 0 \)
\( D = 1^2 — 4 \cdot 1 \cdot (-6) = 1 + 24 = 25 \)
\( x_1 = \frac{-1 + \sqrt{25}}{2 \cdot 1} = \frac{-1 + 5}{2} = \frac{4}{2} = 2 \)
\( x_2 = \frac{-1 — \sqrt{25}}{2 \cdot 1} = \frac{-1 — 5}{2} = \frac{-6}{2} = -3 \)
\( y_1 = 2 — 6 = -4 \)
\( y_2 = -3 — 6 = -9 \)
\((2; -4), (-3; -9)\)
б)
\( y = -x^2 \)
\( x = y + 2 \)
\( y = -(y + 2)^2 \)
\( y = -(y^2 + 4y + 4) \)
\( y = -y^2 — 4y — 4 \)
\( y^2 + 5y + 4 = 0 \)
\( D = 5^2 — 4 \cdot 1 \cdot 4 = 25 — 16 = 9 \)
\( y_1 = \frac{-5 + \sqrt{9}}{2 \cdot 1} = \frac{-5 + 3}{2} = \frac{-2}{2} = -1 \)
\( y_2 = \frac{-5 — \sqrt{9}}{2 \cdot 1} = \frac{-5 — 3}{2} = \frac{-8}{2} = -4 \)
\( x_1 = -1 + 2 = 1 \)
\( x_2 = -4 + 2 = -2 \)
\((1; -1), (-2; -4)\)
Условие:
а) Найти точку на графике \(y = -x^2\), где ордината на 6 меньше абсциссы.
б) Найти точку на графике \(y = -x^2\), где абсцисса на 2 больше ординаты.
Решение:
а)
\(y = -x^2\)
— уравнение параболы
\(y = x — 6\)
— ордината на 6 меньше абсциссы
\(-x^2 = x — 6\)
— приравниваем
\(x^2 + x — 6 = 0\)
— квадратное уравнение
\(D = 1^2 — 4 \cdot 1 \cdot (-6) = 25\)
— дискриминант
\(x_1 = \frac{-1 + \sqrt{25}}{2} = 2\)
— первый корень
\(x_2 = \frac{-1 — \sqrt{25}}{2} = -3\)
— второй корень
\(y_1 = 2 — 6 = -4\)
— ордината для \(x_1\)
\(y_2 = -3 — 6 = -9\)
— ордината для \(x_2\)
Проверка:
\(-x^2 = y\)
\(-2^2 = -4\)
— верно
\(-(-3)^2 = -9\)
— верно
б)
\(y = -x^2\)
— уравнение параболы
\(x = y + 2\)
— абсцисса на 2 больше ординаты
\(x = -x^2 + 2\)
— подставляем \(y\)
\(x^2 + x — 2 = 0\)
— квадратное уравнение
\(D = 1^2 — 4 \cdot 1 \cdot (-2) = 9\)
— дискриминант
\(x_1 = \frac{-1 + \sqrt{9}}{2} = 1\)
— первый корень
\(x_2 = \frac{-1 — \sqrt{9}}{2} = -2\)
— второй корень
\(y_1 = 1 — 2 = -1\)
— ордината для \(x_1\)
\(y_2 = -2 — 2 = -4\)
— ордината для \(x_2\)
Проверка:
\(-x^2 = y\)
\(-1^2 = -1\)
— верно
\(-(-2)^2 = -4\)
— верно
б)
\((1; -1)\), \((-2; -4)\)