Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 21.9 Мордкович — Подробные Ответы
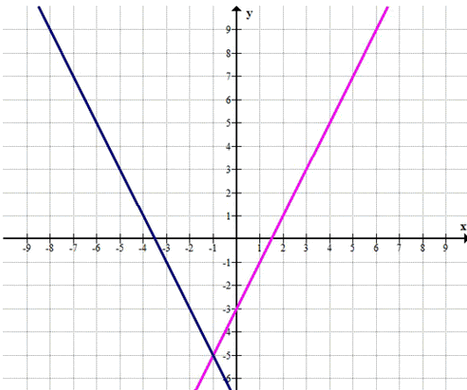
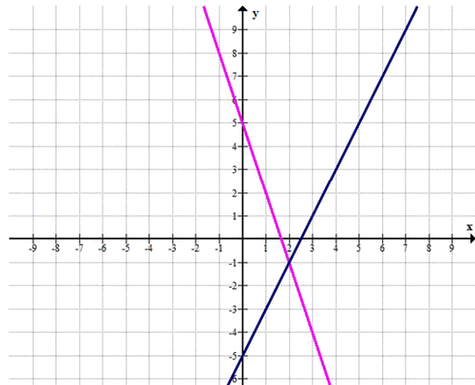
а) Даны линейные функции у = 2х — 3 и у = — 2х + р. При каком значении параметра р значения функций в точках с абсциссой -1 равны? Сделайте чертёж. б) Даны линейные функции у = — 3х + 5 и у = 2х + р. При каком значении р значения функций в точках с абсциссой 2 равны? Сделайте чертёж.
1)
\( y = 2x — 3 \)
\( y = -2x + p \)
\( x = -1 \)
\( 2(-1) — 3 = -2 — 3 = -5 \)
\( -2(-1) + p = 2 + p \)
\( 2 + p = -5 \)
\( p = -5 — 2 \)
\( p = -7 \)
2)
\( y = -3x + 5 \)
\( y = 2x + p \)
\( x = 2 \)
\( -3(2) + 5 = -6 + 5 = -1 \)
\( 2(2) + p = 4 + p \)
\( 4 + p = -1 \)
\( p = -1 — 4 \)
\( p = -5 \)
Условие:
a) Найти \(p\), при котором значения функций \(y = 2x — 3\)
и \(y = -2x + p\)
равны при \(x = -1\).
б) Найти \(p\), при котором значения функций \(y = -3x + 5\)
и \(y = 2x + p\)
равны при \(x = 2\).
Решение:
а)
\(y_1 = 2x — 3\)
— первая функция
\(y_2 = -2x + p\)
— вторая функция
\(x = -1\)
— заданная абсцисса
\(y_1(-1) = 2 \cdot (-1) — 3 = -2 — 3 = -5\)
— значение первой функции
\(y_2(-1) = -2 \cdot (-1) + p = 2 + p\)
— значение второй функции
\(y_1(-1) = y_2(-1)\)
— приравниваем значения
\(-5 = 2 + p\)
— уравнение для \(p\)
\(p = -5 — 2 = -7\)
— находим \(p\)
б)
\(y_1 = -3x + 5\)
— первая функция
\(y_2 = 2x + p\)
— вторая функция
\(x = 2\)
— заданная абсцисса
\(y_1(2) = -3 \cdot 2 + 5 = -6 + 5 = -1\)
— значение первой функции
\(y_2(2) = 2 \cdot 2 + p = 4 + p\)
— значение второй функции
\(y_1(2) = y_2(2)\)
— приравниваем значения
\(-1 = 4 + p\)
— уравнение для \(p\)
\(p = -1 — 4 = -5\)
— находим \(p\)
б)
\(p = -5\)