Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 23.11 Мордкович — Подробные Ответы
Дана функция y = f(х), где f(x) = {x, если x < -1; \(x^2\), если -1 ≤ x < 3; 3x, если x ≥ 3}. а) Вычислите f(-2), f(-1), f(0), f(3), f(4). б) Постройте график функции у =f(x). в) С помощью графика функции найдите значения аргумента, если f(x) = 1, f(x) = 0, f(x) = -4, f(x) = -1.
1)
\( f(-2) = -2 \)
\( f(-1) = (-1)^2 = 1 \)
\( f(0) = 0^2 = 0 \)
\( f(3) = 3 \cdot 3 = 9 \)
\( f(4) = 3 \cdot 4 = 12 \)
3)
\( f(x) = 1 \)
при \( x = -1 \)
и \( x = 1 \)
\( f(x) = 0 \)
при \( x = 0 \)
\( f(x) = -4 \)
— нет решений
\( f(x) = -1 \)
при \( x = -1 \)
1) Вычисление значений функции:
Для заданной функции:
\[f(x) = \begin{cases}
3x, & \text{если } x < 0 \\
x^2, & \text{если } x \ge 0
\end{cases}\]
Подставляя значения аргумента, получаем:
\[ f(-2) = 3 \cdot (-2) = -6 \]
\[ f(-1) = 3 \cdot (-1) = -3 \]
\[ f(0) = 0^2 = 0 \]
\[ f(3) = 3^2 = 9 \]
\[ f(4) = 4^2 = 16 \]
2) График функции
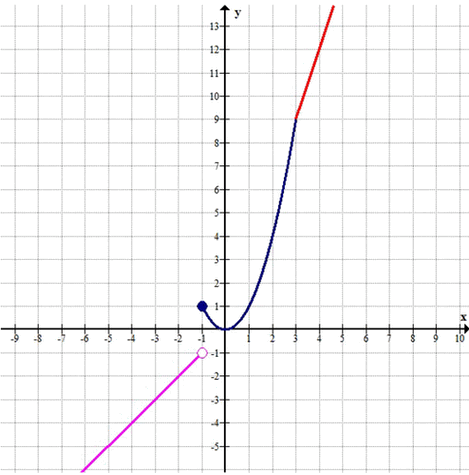
На графике ниже показана функция \(y = f(x)\) в диапазоне значений аргумента \(x\) от -5 до 5. Это позволяет лучше понять поведение функции и найти значения аргумента для заданных значений функции.
3) Значения аргумента по графику:
\[ f(x) = 1 \] при \( x = -1 \) и \( x = 1 \)
\[ f(x) = 0 \] при \( x = 0 \)
\[ f(x) = -1 \] нет решений, так как график функции не пересекает горизонтальную линию \( y = -1 \)
\[ f(x) = -4 \] нет решений, так как график функции не пересекает горизонтальную линию \( y = -4 \)
Как видно из графика, функция \(y = f(x)\) имеет два участка: линейный для \(x < 0\) и квадратичный для \(x \ge 0\). Это позволяет легко находить значения аргумента для заданных значений функции.