ГДЗ по Алгебре 7 Класс Номер 23.14 Мордкович — Подробные Ответы

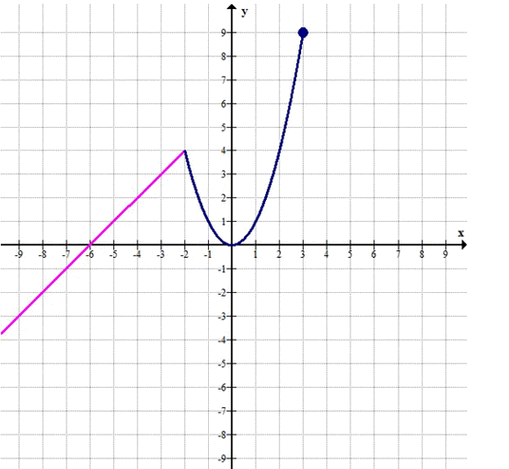
При каких значениях параметра р уравнение f(x) = р, где f(x) = {x + 6, если x ≤ -2; \(x^2\), если -2 < x ≤ 3}: а) имеет один корень; б) имеет два корня; в) имеет не более двух корней; г) имеет три корня; д) не имеет корней; е) имеет хотя бы один корень?

Условие
Найти количество корней уравнения \(f(x) = p\) для кусочной функции:

\[
f(x) = \begin{cases}
x + 6, & x \le -2 \\
x^2, & -2 < x \le 3
\end{cases}
\]

Область значений
— \(f(x) \le 4\) для \(x \le -2\).
— \(4 < f(x) \le 9\) для \(-2 < x \le 3\).
— Общая область: \((-\infty; 9]\).

Количество корней
— Один корень:
— \(p < 4\) — один корень.

— Два корня:
— \(p = 4\) — два корня.
— \(4 < p < 9\) — два корня.

— Три корня:
— \(p = 9\) — один корень.

— Нет корней:
— \(p > 9\) — нет корней.

— Хотя бы один корень:
— \(p \le 9\).

Условие:
Найти количество корней уравнения \(f(x) = p\)
в зависимости от параметра \(p\), где \(f(x)\)
задана кусочно.

Решение:
Рассмотрим функцию \(f(x)\)
на заданных интервалах:

\(f(x) = \begin{cases}
x + 6, & \text{если } x \le -2 \\
x^2, & \text{если } -2 < x \le 3
\end{cases}\)

1. \(x \le -2\): \(f(x) = x + 6\).
При \(x = -2\), \(f(-2) = -2 + 6 = 4\).
Так как \(x\)
может быть любым числом, меньшим или равным \(-2\), то \(f(x)\)может принимать любые значения, меньшие или равные \(4\).
\(f(x) \le 4\)

2. \(-2 < x \le 3\): \(f(x) = x^2\).
При \(x \to -2\), \(f(x) \to 4\).
При \(x = 3\), \(f(3) = 3^2 = 9\).
Так как \(x^2\)
непрерывна на этом интервале, то \(f(x)\)
принимает все значения от \(4\)
(не включая) до \(9\)
(включая).
\(4 < f(x) \le 9\)

Область значений функции \(f(x)\): \((-\infty; 9]\).

а) Один корень:
\(p > 9\)
— функция не определена
\(p < 4\)
— один корень

б) Два корня:
\(p = 4\)
— один корень при \(x=-2\)
и один при \(x \to -2\)

\(4 < p < 9\)
— два корня

в) Не более двух корней:
\(p < 9\)

г) Три корня:
\(p = 9\)
— один корень

д) Нет корней:
\(p > 9\)

е) Имеет хотя бы один корень:
\(p \le 9\)