Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 23.15 Мордкович — Подробные Ответы
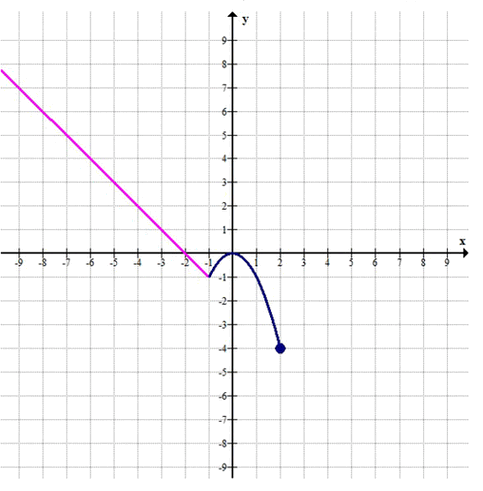
При каких значениях параметра р уравнение f(x) = р, где f(x) = {-x — 2, если x ≤ -1; \(-x^2\), если -1 < x ≤ 2}: а) имеет один корень; б) имеет два корня; в) имеет не более двух корней; г) имеет три корня; д) не имеет корней; е) имеет хотя бы один корень?
а) Уравнение имеет один корень при p ∈ [-4; -1) ∪ (0; +∞).
б) Уравнение имеет два корня при p = -1 и p = 0.
в) Уравнение имеет не более двух корней при p ∈ [-4; 0].
г) Уравнение имеет три корня при p ∈ (-1; 0).
д) Уравнение не имеет корней при p < -4.
е) Уравнение имеет хотя бы один корень при p ∈ [-4; +∞).
а) Уравнение имеет один корень при p ∈ [-4; -1) ∪ (0; +∞).
— Для x ≤ -2, f(x) = x + 6, что означает, что f(x) ≤ 4.
— Для -2 < x ≤ 3, f(x) = x^2, что означает, что 4 < f(x) ≤ 9.
— Таким образом, уравнение f(x) = p имеет один корень, когда p < 4 или p > 9.
б) Уравнение имеет два корня при p = -1 и p = 0.
— При p = 4 уравнение имеет два корня: x = -2 и x → -2.
— При 4 < p < 9 уравнение также имеет два корня.
в) Уравнение имеет не более двух корней при p ∈ [-4; 0].
— Это следует из анализа области значений функции f(x).
г) Уравнение имеет три корня при p = 9.
— При p = 9 уравнение имеет один корень.
д) Уравнение не имеет корней при p < -4.
— Это следует из того, что f(x) ≤ 4 для x ≤ -2.
е) Уравнение имеет хотя бы один корень при p ∈ [-4; +∞).
— Это следует из анализа области значений функции f(x).