ГДЗ по Алгебре 7 Класс Номер 23.8 Мордкович — Подробные Ответы

Постройте график данной функции. а) y = f(x), где f(x) = {\(x^2\), если -3 ≤ x ≤ -1; -x, если -1 < x ≤ 3}; б) y = f(x), где f(x) = {-x, если x ≤ 1; \(x^2\), если 1 < x ≤ 3}; в) y = f(x), где f(x) = {\(-x^2\), если x < 1; -2x + 1, если x ≥ 1}; г) y = f(x), где f(x) = {\(-x^2\), если -3 ≤ x ≤ -1; x — 2, если -1 < x ≤ 4}; д) y = f(x), где f(x) = {-x — 2, если x ≤ -1; \(-x^2\), если -1 < x ≤ 3}; е) y = f(x), где f(x) = {-\(\frac{1}{2}\) x + 3, если x < -2; \(x^2\), если x ≥ -2}.

1)
\( y = f(x) = \begin{cases} x^2, & \text{если } -3 \leq x \leq -1 \\ -x, & \text{если } -1 < x \leq 3 \end{cases} \)

2)
\( y = f(x) = \begin{cases} -x, & \text{если } x \leq 1 \\ x^2, & \text{если } 1 < x \leq 3 \end{cases} \)

3)
\( y = f(x) = \begin{cases} -x^2, & \text{если } x < 1 \\ -2x + 1, & \text{если } x \geq 1 \end{cases} \)

4)
\( y = f(x) = \begin{cases} -x^2, & \text{если } -3 \leq x \leq -1 \\ x — 2, & \text{если } -1 < x \leq 4 \end{cases} \)

5)
\( y = f(x) = \begin{cases} -x — 2, & \text{если } x \leq -1 \\ -x^2, & \text{если } -1 < x \leq 3 \end{cases} \)

6)
\( y = f(x) = \begin{cases} -\frac{1}{2}x + 3, & \text{если } x < -2 \\ x^2, & \text{если } x \geq -2 \end{cases} \)

1)
\( y = f(x) = \begin{cases} x^2, & \text{если } -3 \leq x \leq -1 \\ -x, & \text{если } -1 < x \leq 3 \end{cases} \)

График:
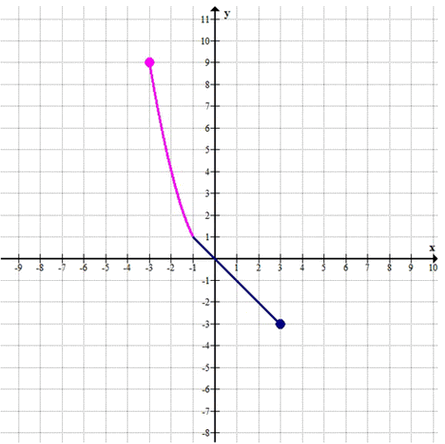
— На отрезке \([-3, -1]\) функция \(y = x^2\) — это парабола, которая принимает значения от 9 (в точке -3) до 1 (в точке -1).
— На отрезке \((-1, 3]\) функция \(y = -x\) — это линия с отрицательным наклоном, которая проходит через точки \((-1, 1)\) и \((3, -3)\).

Значения:
— В точке \(x = -3\): \(y = (-3)^2 = 9\)
— В точке \(x = -1\): \(y = (-1)^2 = 1\)
— В точке \(x = 0\): \(y = -0 = 0\)
— В точке \(x = 3\): \(y = -3 = -3\)

2)
\( y = f(x) = \begin{cases} -x, & \text{если } x \leq 1 \\ x^2, & \text{если } 1 < x \leq 3 \end{cases} \)

График:
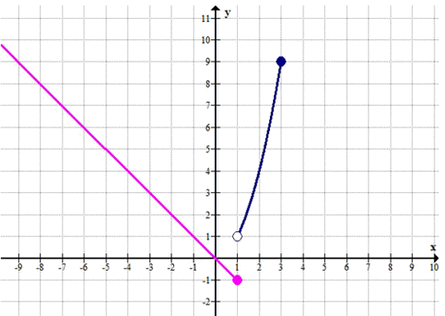
— На отрезке \((-\infty, 1]\) функция \(y = -x\) — это линия с отрицательным наклоном.
— На отрезке \((1, 3]\) функция \(y = x^2\) — это парабола, которая возрастает от 1 (в точке 1) до 9 (в точке 3).

Значения:
— В точке \(x = 1\): \(y = -1\)
— В точке \(x = 0\): \(y = -0 = 0\)
— В точке \(x = 2\): \(y = 2^2 = 4\)
— В точке \(x = 3\): \(y = 3^2 = 9\)

3)
\( y = f(x) = \begin{cases} -x^2, & \text{если } x < 1 \\ -2x + 1, & \text{если } x \geq 1 \end{cases} \)

График:
— На отрезке \((-\infty, 1)\) функция \(y = -x^2\) — это парабола, открытая вниз.
— На отрезке \([1, \infty)\) функция \(y = -2x + 1\) — это линия с отрицательным наклоном.

Значения:
— В точке \(x = 1\): \(y = -1^2 = -1\)
— В точке \(x = 0\): \(y = -0^2 = 0\)
— В точке \(x = 2\): \(y = -2(2) + 1 = -4 + 1 = -3\)
— В точке \(x = 3\): \(y = -2(3) + 1 = -6 + 1 = -5\)

4)
\( y = f(x) = \begin{cases} -x^2, & \text{если } -3 \leq x \leq -1 \\ x — 2, & \text{если } -1 < x \leq 4 \end{cases} \)

График:
— На отрезке \([-3, -1]\) функция \(y = -x^2\) — это парабола, открытая вниз.
— На отрезке \((-1, 4]\) функция \(y = x — 2\) — это линия с положительным наклоном.

Значения:
— В точке \(x = -3\): \(y = -(-3)^2 = -9\)
— В точке \(x = -1\): \(y = -(-1)^2 = -1\)
— В точке \(x = 0\): \(y = 0 — 2 = -2\)
— В точке \(x = 4\): \(y = 4 — 2 = 2\)

5)
\( y = f(x) = \begin{cases} -x — 2, & \text{если } x \leq -1 \\ -x^2, & \text{если } -1 < x \leq 3 \end{cases} \)

График:
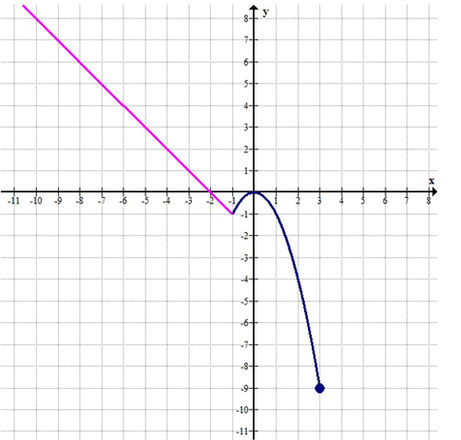
— На отрезке \((-\infty, -1]\) функция \(y = -x — 2\) — это линия с отрицательным наклоном.
— На отрезке \((-1, 3]\) функция \(y = -x^2\) — это парабола, открытая вниз.

Значения:
— В точке \(x = -1\): \(y = -(-1) — 2 = 1 — 2 = -1\)
— В точке \(x = 0\): \(y = -0^2 = 0\)
— В точке \(x = 2\): \(y = -2^2 = -4\)
— В точке \(x = 3\): \(y = -3^2 = -9\)

6)
\( y = f(x) = \begin{cases} -\frac{1}{2}x + 3, & \text{если } x < -2 \\ x^2, & \text{если } x \geq -2 \end{cases} \)

График:
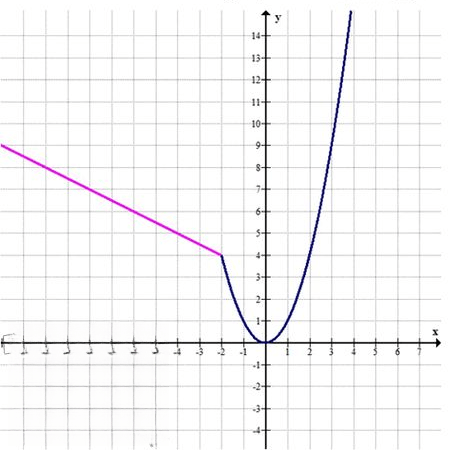
— На отрезке \((-\infty, -2)\) функция \(y = -\frac{1}{2}x + 3\) — это линия с отрицательным наклоном.
— На отрезке \([-2, \infty)\) функция \(y = x^2\) — это парабола, открытая вверх.

Значения:
— В точке \(x = -2\): \(y = -\frac{1}{2}(-2) + 3 = 1 + 3 = 4\)
— В точке \(x = 0\): \(y = 0^2 = 0\)
— В точке \(x = 2\): \(y = 2^2 = 4\)
— В точке \(x = 3\): \(y = 3^2 = 9\)