Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 25.16 Мордкович — Подробные Ответы
Постройте график функции:
а)
\(y = \frac{x^3}{x}\);
б)
\(y = -\frac{x^4}{x}\).
Условие: Построить график функции:
а)
\(y = \frac{x^3}{x}\);
б)
\(y = -\frac{x^4}{x}\).
Решение:
а)
\(y = \frac{x^3}{x}\)
\(y = x^2\)
— упрощение функции, при \(x \neq 0\)
\(x = 0\)
— точка разрыва
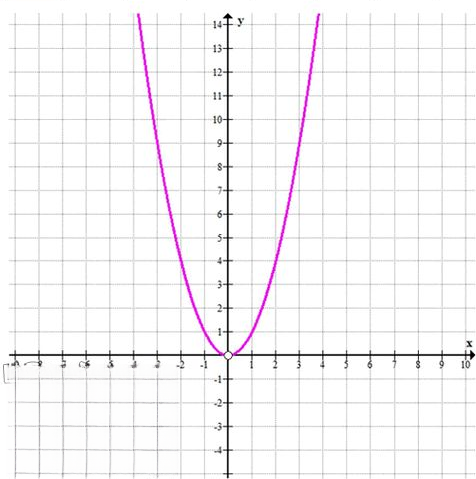
График: парабола \(y = x^2\)
с выколотой точкой в \(x = 0\).
б)
\(y = -\frac{x^4}{x}\)
\(y = -x^3\)
— упрощение функции, при \(x \neq 0\)
\(x = 0\)
— точка разрыва
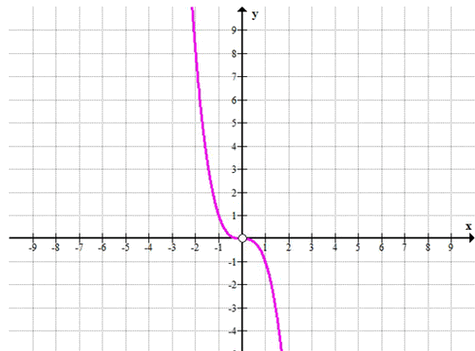
График: кубическая парабола \(y = -x^3\)
с выколотой точкой в \(x = 0\).
а) Функция: \(y = \frac{x^3}{x}\)
Шаги анализа:
1. Упрощение функции:
\(y = \frac{x^3}{x} = x^2\), при \(x \neq 0\)
Это связано с тем, что при делении \(x^3\) на \(x\), \(x\) сокращается, и мы получаем \(x^2\).
2. Точка разрыва:
При \(x = 0\) функция не определена, так как деление на 0 не допускается. Поэтому в точке \(x = 0\) функция имеет разрыв.
Таким образом, функция \(y = \frac{x^3}{x}\) при \(x \neq 0\) упрощается до \(y = x^2\), а в точке \(x = 0\) имеет разрыв.
б) Функция: \(y = -\frac{x^4}{x}\)
Шаги анализа:
1. Упрощение функции:
\(y = -\frac{x^4}{x} = -x^3\), при \(x \neq 0\)
Это связано с тем, что при делении \(x^4\) на \(x\), \(x\) сокращается, и мы получаем \(x^3\).
2. Точка разрыва:
При \(x = 0\) функция не определена, так как деление на 0 не допускается. Поэтому в точке \(x = 0\) функция имеет разрыв.
Таким образом, функция \(y = -\frac{x^4}{x}\) при \(x \neq 0\) упрощается до \(y = -x^3\), а в точке \(x = 0\) имеет разрыв.