ГДЗ по Алгебре 7 Класс Номер 29.23 Мордкович — Подробные Ответы

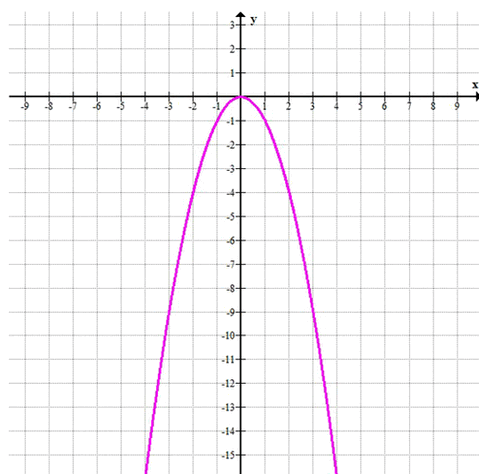
Постройте график функции \(у = —х^2\). Найдите: а) наименьшее и наибольшее значения функции на отрезке [-\(\frac{1}{2}\); 1]; б) значения x, при которых у = —2 \(\frac{1}{4}\).

\( y = -x^2 \)

а)
\( x = -\frac{1}{2} \)

\( y = -\left(-\frac{1}{2}\right)^2 = -\frac{1}{4} \)

\( x = 1 \)

\( y = -(1)^2 = -1 \)

Наибольшее значение: \( y = 0 \)
при \( x = 0 \)

Наименьшее значение: \( y = -1 \)

б)
\( y = -2\frac{1}{4} = -\frac{9}{4} \)

\( -\frac{9}{4} = -x^2 \)

\( x^2 = \frac{9}{4} \)

\( x = \pm \sqrt{\frac{9}{4}} = \pm \frac{3}{2} \)

\( x = \pm 1\frac{1}{2} \)

Условие: Построить график \(y = -x^2\), найти наименьшее и наибольшее значения на \([-\frac{1}{2}; 1]\)
и значения \(x\)
при \(y = -2\frac{1}{4}\).

Решение:
График функции \(y = -x^2\)
— парабола, ветви направлены вниз.

а) Наименьшее и наибольшее значения на отрезке \([-\frac{1}{2}; 1]\):
\(x = 0\)
— вершина параболы
\(y(0) = -0^2 = 0\)
— наибольшее значение

\(y(-\frac{1}{2}) = -(-\frac{1}{2})^2 = -\frac{1}{4}\)
— значение на левом конце отрезка
\(y(1) = -1^2 = -1\)
— значение на правом конце отрезка

Наименьшее значение на отрезке: \(y(1) = -1\)

б) Значения \(x\), при которых \(y = -2\frac{1}{4}\):
\( -x^2 = -2\frac{1}{4} \)
— уравнение
\( x^2 = \frac{9}{4} \)
— умножили на -1
\( x = \pm \sqrt{\frac{9}{4}} \)
— извлекаем корень
\( x = \pm \frac{3}{2} \)
— корни

Ответ:

а) Наибольшее: \(0\), наименьшее: \(-1\)

б)
\(x = \frac{3}{2}\), \(x = -\frac{3}{2}\)