Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 34.15 Мордкович — Подробные Ответы
Постройте график уравнения: а) х(х — у) = 0; г) y(x + y) = 0; б) (x — 4)(у + 3) = 0; д) (x + 1)(y — 2) = 0; в) (х — 3)(x — у) = 0; е) (y + 2)(x + y) = 0.
а)
\( x(x — y) = 0 \)
\( x = 0 \)
\( x — y = 0 \Rightarrow y = x \)
б)
\( (x — 4)(y + 3) = 0 \)
\( x — 4 = 0 \Rightarrow x = 4 \)
\( y + 3 = 0 \Rightarrow y = -3 \)
в)
\( (x — 3)(x — y) = 0 \)
\( x — 3 = 0 \Rightarrow x = 3 \)
\( x — y = 0 \Rightarrow y = x \)
г)
\( y(x + y) = 0 \)
\( y = 0 \)
\( x + y = 0 \Rightarrow y = -x \)
д)
\( (x + 1)(y — 2) = 0 \)
\( x + 1 = 0 \Rightarrow x = -1 \)
\( y — 2 = 0 \Rightarrow y = 2 \)
е)
\( (y + 2)(x + y) = 0 \)
\( y + 2 = 0 \Rightarrow y = -2 \)
\( x + y = 0 \Rightarrow y = -x \)
Условие:
Построить графики уравнений:
а)
\(x(x — y) = 0\);
б)
\((x — 4)(y + 3) = 0\);
в)
\((x — 3)(x — y) = 0\);
г)
\(y(x + y) = 0\);
д)
\((x + 1)(y — 2) = 0\);
е)
\((y + 2)(x + y) = 0\).
Решение:
а)
\(x(x — y) = 0\)
\(x = 0\)
или \(x — y = 0\)
\(x = 0\)
или \(y = x\)
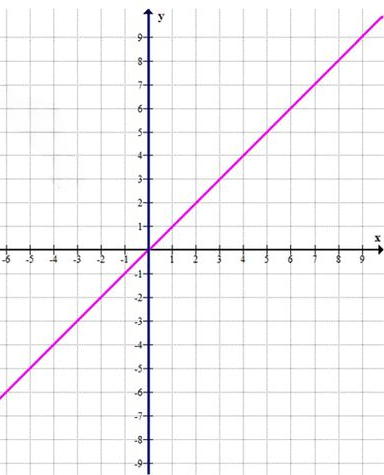
График: прямая \(x = 0\)
(ось y) и прямая \(y = x\).
б)
\((x — 4)(y + 3) = 0\)
\(x — 4 = 0\)
или \(y + 3 = 0\)
\(x = 4\)
или \(y = -3\)
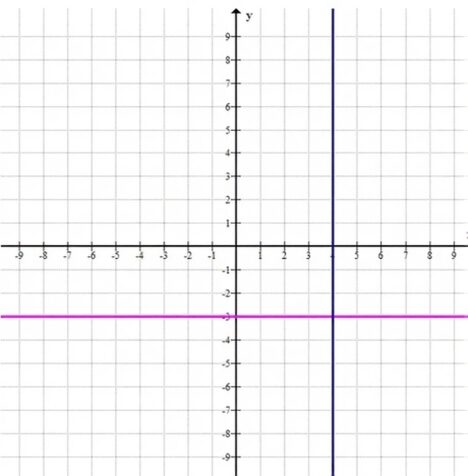
График: прямая \(x = 4\)
и прямая \(y = -3\).
в)
\((x — 3)(x — y) = 0\)
\(x — 3 = 0\)
или \(x — y = 0\)
\(x = 3\)
или \(y = x\)
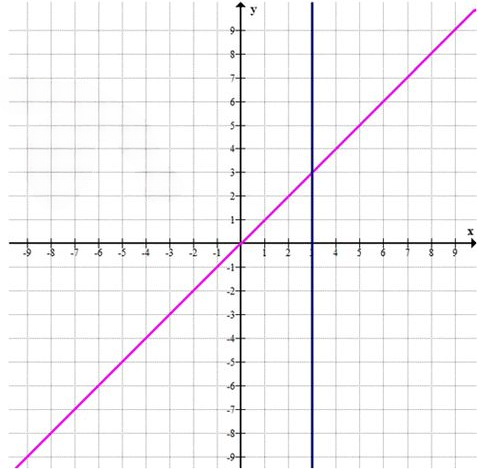
График: прямая \(x = 3\)
и прямая \(y = x\).
г)
\(y(x + y) = 0\)
\(y = 0\)
или \(x + y = 0\)
\(y = 0\)
или \(y = -x\)
График: прямая \(y = 0\)
(ось x) и прямая \(y = -x\).
д)
\((x + 1)(y — 2) = 0\)
\(x + 1 = 0\)
или \(y — 2 = 0\)
\(x = -1\)
или \(y = 2\)
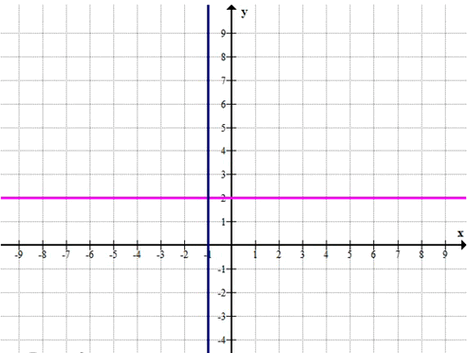
График: прямая \(x = -1\)
и прямая \(y = 2\).
е)
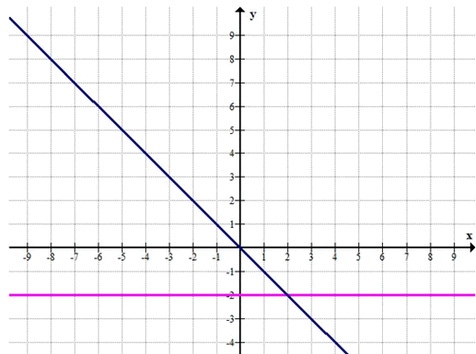
\((y + 2)(x + y) = 0\)
\(y + 2 = 0\)
или \(x + y = 0\)
\(y = -2\)
или \(y = -x\)
График: прямая \(y = -2\)
и прямая \(y = -x\).
Ответы:
а)
\(x = 0\), \(y = x\)
б)
\(x = 4\), \(y = -3\)
в)
\(x = 3\), \(y = x\)
г)
\(y = 0\), \(y = -x\)
д)
\(x = -1\), \(y = 2\)
е)
\(y = -2\), \(y = -x\)