Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 35.18 Мордкович — Подробные Ответы
Постройте график уравнения: а) \((x + 1)^2\) — \(y^{2}\) = 0; б) \((x — 3)^2 — (y + 2)^2\) = 0; \(в) (x — 2)^2 = (y + 2)^2\); г) \(x^{2}\) — \((y — 2)^2\) = 0; д) (x + \(4)^2 — (y — 1)^2 = 0; е) (x + 1)^2 = (y — 4)^2\).
а)
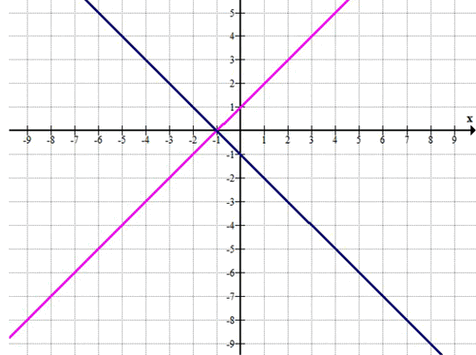
\( (x+1)^2 — y^2 = 0 \)
\( (x+1-y)(x+1+y) = 0 \)
\( x+1-y = 0 \)или \( x+1+y = 0 \)
\( y = x+1 \)или \( y = -x-1 \)
б)
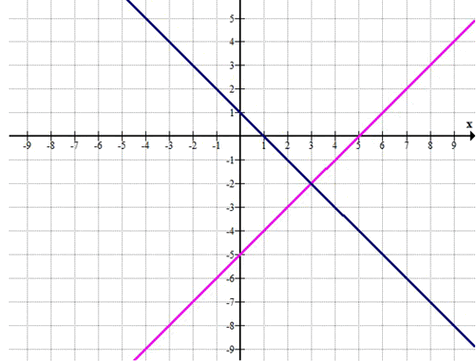
\( (x-3)^2 — (y+2)^2 = 0 \)
\( (x-3-y-2)(x-3+y+2) = 0 \)
\( (x-y-5)(x+y-1) = 0 \)
\( x-y-5 = 0 \)или \( x+y-1 = 0 \)
\( y = x-5 \)или \( y = -x+1 \)
в)
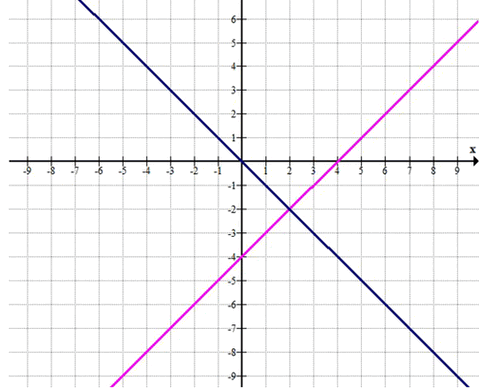
\( (x-2)^2 = (y+2)^2 \)
\( (x-2)^2 — (y+2)^2 = 0 \)
\( (x-2-y-2)(x-2+y+2) = 0 \)
\( (x-y-4)(x+y) = 0 \)
\( x-y-4 = 0 \)или \( x+y = 0 \)
\( y = x-4 \)или \( y = -x \)
г)
\( x^2 — (y-2)^2 = 0 \)
\( (x-y+2)(x+y-2) = 0 \)
\( x-y+2 = 0 \)или \( x+y-2 = 0 \)
\( y = x+2 \)или \( y = -x+2 \)
д)
\( (x+4)^2 — (y-1)^2 = 0 \)
\( (x+4-y+1)(x+4+y-1) = 0 \)
\( (x-y+5)(x+y+3) = 0 \)
\( x-y+5 = 0 \)или \( x+y+3 = 0 \)
\( y = x+5 \)или \( y = -x-3 \)
е)
\( (x+1)^2 = (y-4)^2 \)
\( (x+1)^2 — (y-4)^2 = 0 \)
\( (x+1-y+4)(x+1+y-4) = 0 \)
\( (x-y+5)(x+y-3) = 0 \)
\( x-y+5 = 0 \)или \( x+y-3 = 0 \)
\( y = x+5 \)или \( y = -x+3 \)
Условие: Построить график уравнения вида \( (x — a)^2 — (y — b)^2 = 0 \)и \( (x — a)^2 = (y — b)^2 \).
Решение:
а)
\( (x + 1)^2 — y^2 = 0 \)
\( (x + 1)^2 = y^2 \)
— приводим к виду квадратов
\( x + 1 = \pm y \)
— извлекаем корень
\( y = x + 1 \)
или \( y = -x — 1 \)
— два уравнения прямых
б)
\( (x — 3)^2 — (y + 2)^2 = 0 \)
\( (x — 3)^2 = (y + 2)^2 \)
— приводим к виду квадратов
\( x — 3 = \pm (y + 2) \)
— извлекаем корень
\( y + 2 = x — 3 \)или \( y + 2 = -x + 3 \)
— два случая
\( y = x — 5 \)или \( y = -x + 1 \)
— два уравнения прямых
в)
\( (x — 2)^2 = (y + 2)^2 \)
\( x — 2 = \pm (y + 2) \)
— извлекаем корень
\( y + 2 = x — 2 \)или \( y + 2 = -x + 2 \)
— два случая
\( y = x — 4 \)или \( y = -x \)
— два уравнения прямых
г)
\( x^2 — (y — 2)^2 = 0 \)
\( x^2 = (y — 2)^2 \)
— приводим к виду квадратов
\( x = \pm (y — 2) \)
— извлекаем корень
\( y — 2 = x \)или \( y — 2 = -x \)
— два случая
\( y = x + 2 \)или \( y = -x + 2 \)
— два уравнения прямых
д)
\( (x + 4)^2 — (y — 1)^2 = 0 \)
\( (x + 4)^2 = (y — 1)^2 \)
— приводим к виду квадратов
\( x + 4 = \pm (y — 1) \)
— извлекаем корень
\( y — 1 = x + 4 \)или \( y — 1 = -x — 4 \)
— два случая
\( y = x + 5 \)или \( y = -x — 3 \)
— два уравнения прямых
е)
\( (x + 1)^2 = (y — 4)^2 \)
\( x + 1 = \pm (y — 4) \)
— извлекаем корень
\( y — 4 = x + 1 \)или \( y — 4 = -x — 1 \)
— два случая
\( y = x + 5 \)или \( y = -x + 3 \)
— два уравнения прямых
Графиком каждого уравнения является пара пересекающихся прямых.