Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 36.21 Мордкович — Подробные Ответы
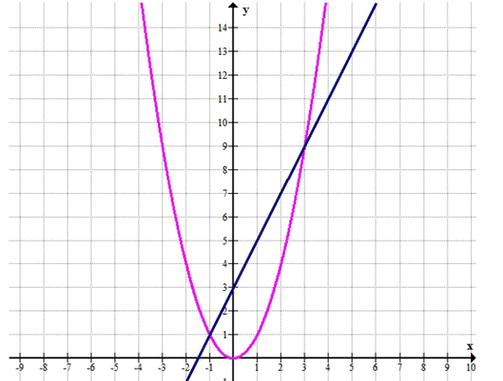
Решите графически уравнение и укажите корень уравнения, принадлежащий заданному числовому промежутку: а) \(х^{2}\) = 2х + 3, (-2; 1); б) -\(х^{2}\) = 3x, [-3; 0).
a)
\( y = x^2 \)
\( y = 2x + 3 \)
\( x^2 = 2x + 3 \)
\( x^2 — 2x — 3 = 0 \)
\( (x — 3)(x + 1) = 0 \)
\( x_1 = 3 \)
\( x_2 = -1 \)
\( x \in (-2; 1) \)
\( x = -1 \)
б)
\( y = -x^2 \)
\( y = 3x \)
\( -x^2 = 3x \)
\( x^2 + 3x = 0 \)
\( x(x + 3) = 0 \)
\( x_1 = 0 \)
\( x_2 = -3 \)
\( x \in [-3; 0) \)
\( x = -3 \)
Условие: Решить графически уравнения \(x^2 = 2x + 3\) и \(-x^2 = 3x\)
и найти корни в заданных промежутках.
Решение:
а)
\(x^2 = 2x + 3\), промежуток \((-2; 1)\)
\( y = x^2 \)
— парабола
\( y = 2x + 3 \)
— прямая
Графическое решение: строим параболу и прямую, находим точки пересечения.
Точки пересечения: \( (-1; 1) \) и \( (3; 9) \)
\( x_1 = -1 \)
— корень уравнения
\( x_2 = 3 \)
— корень уравнения
Проверяем принадлежность корней промежутку \((-2; 1)\):
\( -1 \in (-2; 1) \)
\( 3 \notin (-2; 1) \)
б)
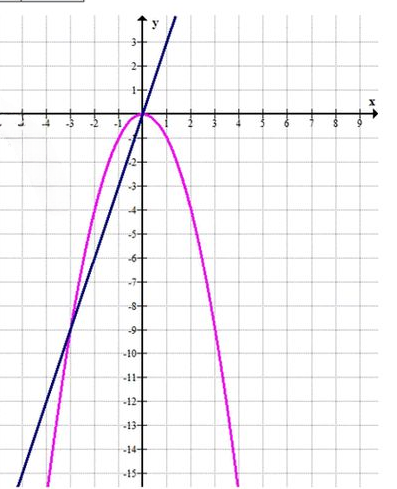
\(-x^2 = 3x\), промежуток \([-3; 0)\)
\( y = -x^2 \)
— парабола
\( y = 3x \)
— прямая
Графическое решение: строим параболу и прямую, находим точки пересечения.
Точки пересечения: \( (0; 0) \)и \( (-3; -9) \)
\( x_1 = 0 \)
— корень уравнения
\( x_2 = -3 \)
— корень уравнения
Проверяем принадлежность корней промежутку \([-3; 0)\):
\( 0 \notin [-3; 0) \)
\( -3 \in [-3; 0) \)
Ответы:
а)
\( -1 \)
б)
\( -3 \)