ГДЗ по Алгебре 7 Класс Номер 38.11 Мордкович — Подробные Ответы

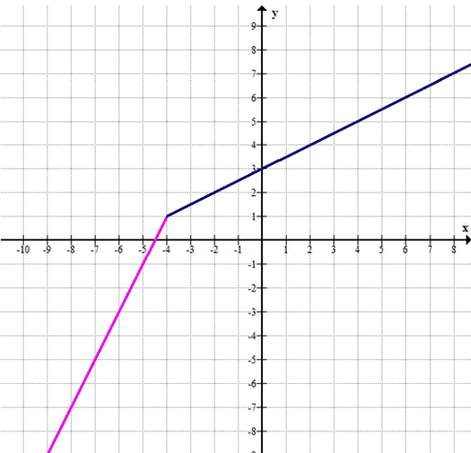
Постройте график функции у = f(x), где f(x) = {2x + 9, если x ≤ -4; \(\frac{1}{2}\) x + 3, если x > -4}. С помощью графика найдите: а) наибольшее значение функции на отрезке [-5; —2]; б) наименьшее значение функции на полуинтервале [—5; 2); в) значение функции в точках —7; —2; 0; 1.

1)
\( y = 2x + 9 \)

\( x = -5 \), \( y = 2 \cdot (-5) + 9 = -1 \)

\( x = -4 \), \( y = 2 \cdot (-4) + 9 = 1 \)

2)
\( y = \frac{1}{2}x + 3 \)

\( x = -4 \), \( y = \frac{1}{2} \cdot (-4) + 3 = 1 \)

\( x = 2 \), \( y = \frac{1}{2} \cdot 2 + 3 = 4 \)

a)
\( f(-4) = 1 \)

\( f(-5) = -1 \)

\( \max_{x \in [-5; -2]} f(x) = f(-4) = 1 \)

б)
\( \min_{x \in [-5; 2)} f(x) = f(-5) = -1 \)

в)
\( f(-7) = 2 \cdot (-7) + 9 = -5 \)

\( f(-2) = \frac{1}{2} \cdot (-2) + 3 = 2 \)

\( f(0) = \frac{1}{2} \cdot 0 + 3 = 3 \)

\( f(1) = \frac{1}{2} \cdot 1 + 3 = 3.5 \)

Условие:
Построить график функции \(f(x)\), заданной кусочно, и найти значения.

Решение:
Построим график функции \(y = f(x)\).

1. Рассмотрим функцию \(y = 2x + 9\)
при \(x \le -4\).
Это линейная функция.

2. Найдем значения в крайних точках:
\(x = -4\): \(y = 2(-4) + 9 = 1\)

\(x = -5\): \(y = 2(-5) + 9 = -1\)

3. Рассмотрим функцию \(y = \frac{1}{2}x + 3\)
при \(x > -4\).
Это тоже линейная функция.

4. Найдем значение в точке, близкой к \(x = -4\):
\(x = -4 + \epsilon\): \(y \approx \frac{1}{2}(-4) + 3 = 1\)

5. Найдем значение в точке \(x = 2\):
\(x = 2\): \(y = \frac{1}{2}(2) + 3 = 4\)

6.

а) Наибольшее значение на отрезке \([-5; -2]\):
На этом отрезке функция \(f(x) = 2x + 9\)
возрастает.
\(f(-2) = 2(-2) + 9 = 5\)

7.

б) Наименьшее значение на полуинтервале \([-5; 2)\):
На этом полуинтервале функция убывает.
\(f(-5) = 2(-5) + 9 = -1\)

8. в) Значения функции в точках:
\(f(-7) = 2(-7) + 9 = -5\)

\(f(-2) = 2(-2) + 9 = 5\)

\(f(0) = \frac{1}{2}(0) + 3 = 3\)

\(f(1) = \frac{1}{2}(1) + 3 = 3.5\)

Ответы:

а) 5;

б) -1;

в)
\(f(-7) = -5\), \(f(-2) = 5\), \(f(0) = 3\), \(f(1) = 3.5\)