Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 39.9 Мордкович — Подробные Ответы
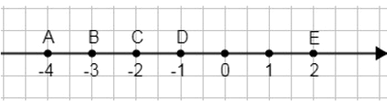
а) На координатной прямой отметьте точки А(—4), В(—3), С(—2), D(-1), Е(2). б) Выпишите ряд данных, состоящий из расстояний между всеми этими точками. в) Сколько всего данных в этом ряду? г) Сколько всего различных данных в этом ряду? д) Укажите самое частое данное. е) Укажите данные, встретившиеся реже всего
а)
— Точка A имеет координату -4
— Точка B имеет координату -3
— Точка C имеет координату -2
— Точка D имеет координату -1
— Точка E имеет координату 2
б)
\(AB = |-3 — (-4)| = 1\)
\(AC = |-2 — (-4)| = 2\)
\(AD = |-1 — (-4)| = 3\)
\(AE = |2 — (-4)| = 6\)
\(BC = |-2 — (-3)| = 1\)
\(BD = |-1 — (-3)| = 2\)
\(BE = |2 — (-3)| = 5\)
\(CD = |-1 — (-2)| = 1\)
\(CE = |2 — (-2)| = 4\)
\(DE = |2 — (-1)| = 3\)
Ряд данных: 1, 2, 3, 6, 1, 2, 5, 1, 4, 3
в) 10
г) 1, 2, 3, 4, 5, 6 — всего 6
д) 1
е) 4, 5, 6
Условие:
На координатной прямой отмечены пять точек: A(-4), B(-3), C(-2), D(-1), E(2). Необходимо вычислить все попарные расстояния между этими точками, определить общее количество расстояний, количество различных расстояний, найти самое частое расстояние и расстояния, встречающиеся реже всего.
Решение:
а) Расположение точек на координатной прямой:
На координатной прямой отмечены пять точек со следующими координатами:
— Точка A имеет координату -4
— Точка B имеет координату -3
— Точка C имеет координату -2
— Точка D имеет координату -1
— Точка E имеет координату 2
При визуальном представлении эти точки располагаются на прямой в порядке возрастания координат: A(-4), B(-3), C(-2), D(-1), E(2). Расстояние между точками E и D составляет 3 единицы, так как между ними находятся три единичных отрезка.
б) Вычисление расстояний между точками:
Расстояние между двумя точками на координатной прямой вычисляется как модуль разности их координат. Рассчитаем расстояния для всех возможных пар точек (всего пар из 5 точек: C(5,2) = 10 пар):
1. Расстояние AB = |B — A| = |-3 — (-4)| = |1| = 1
2. Расстояние AC = |C — A| = |-2 — (-4)| = |2| = 2
3. Расстояние AD = |D — A| = |-1 — (-4)| = |3| = 3
4. Расстояние AE = |E — A| = |2 — (-4)| = |6| = 6
5. Расстояние BC = |C — B| = |-2 — (-3)| = |1| = 1
6. Расстояние BD = |D — B| = |-1 — (-3)| = |2| = 2
7. Расстояние BE = |E — B| = |2 — (-3)| = |5| = 5
8. Расстояние CD = |D — C| = |-1 — (-2)| = |1| = 1
9. Расстояние CE = |E — C| = |2 — (-2)| = |4| = 4
10. Расстояние DE = |E — D| = |2 — (-1)| = |3| = 3
Таким образом, получаем следующие расстояния: 1, 2, 3, 6, 1, 2, 5, 1, 4, 3.
в) Общее количество расстояний:
Всего было вычислено 10 расстояний. Это соответствует количеству всех возможных пар из пяти точек: C(5,2) = 5!/(2!·3!) = (5×4)/(2×1) = 10.
г) Количество различных расстояний:
Из вычисленных 10 расстояний выделим различные значения. Уникальными значениями являются: 1, 2, 3, 4, 5, 6. Таким образом, имеется 6 различных расстояний.
д) Самое частое расстояние:
Подсчитаем частоту каждого расстояния:
— Расстояние 1 встречается 3 раза (AB, BC, CD)
— Расстояние 2 встречается 2 раза (AC, BD)
— Расстояние 3 встречается 2 раза (AD, DE)
— Расстояние 4 встречается 1 раз (CE)
— Расстояние 5 встречается 1 раз (BE)
— Расстояние 6 встречается 1 раз (AE)
Самым частым расстоянием является 1, так как оно встречается 3 раза. Это максимальная частота среди всех расстояний.
е) Расстояния, встретившиеся реже всего:
Расстояния, которые встречаются только один раз, являются самыми редкими. К таким расстояниям относятся: 4, 5, 6. Каждое из этих расстояний встречается только один раз в наборе из 10 расстояний.
Итоговые ответы:
а) Точки отмечены на координатной прямой с координатами A(-4), B(-3), C(-2), D(-1), E(2)
б) Расстояния между точками: 1, 2, 3, 6, 1, 2, 5, 1, 4, 3
в) Общее количество расстояний: 10
г) Количество различных расстояний: 6
д) Самое частое расстояние: 1
е) Расстояния, встретившиеся реже всего: 4, 5, 6
Дополнительный анализ:
Интересно отметить закономерности в распределении расстояний. Точки A, B, C, D расположены последовательно с интервалом в 1 единицу, поэтому расстояния между соседними точками (AB, BC, CD) равны 1. Это объясняет, почему расстояние 1 встречается чаще всего (3 раза). Точка E находится на расстоянии 2 от D, но между E и остальными точками расстояния больше. Различные расстояния от 1 до 6 покрывают диапазон возможных расстояний между этими пятью точками. Наиболее редкие расстояния (4, 5, 6) соответствуют парам, включающим точку E и одну из самых левых точек (A, B, C). Такой анализ расстояний может быть полезен в различных геометрических и комбинаторных задачах, связанных с расположением точек на прямой.