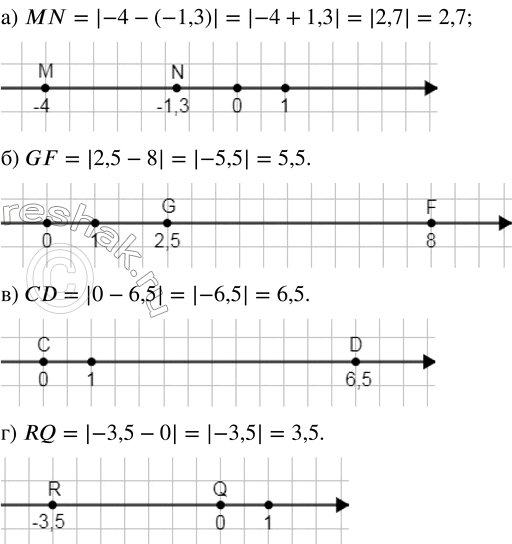Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 6.3 Мордкович — Подробные Ответы
а) Точки \(M(-4)\) и \(N(-1{,}3)\)
Расстояние между двумя точками на координатной прямой вычисляется как модуль разности их координат:
\[
MN = \left| -4 — (-1{,}3) \right| = \left| -4 + 1{,}3 \right| = \left| -2{,}7 \right| = 2{,}7
\]
На координатной прямой:
— точка \(M\) находится в точке \(-4\);
— точка \(N\) — в точке \(-1{,}3\);
— расстояние между ними — \(2{,}7\) единичных отрезка.
б) Точки \(G(2{,}5)\) и \(F(8)\)
\[
GF = \left| 2{,}5 — 8 \right| = \left| -5{,}5 \right| = 5{,}5
\]
На координатной прямой:
— точка \(G\) — в точке \(2{,}5\);
— точка \(F\) — в точке \(8\);
— расстояние — \(5{,}5\) единиц.
в) Точки \(C(0)\) и \(B(6{,}5)\)
\[
CB = \left| 0 — 6{,}5 \right| = \left| -6{,}5 \right| = 6{,}5
\]
На координатной прямой:
— точка \(C\) — в начале координат, \(0\);
— точка \(B\) — в точке \(6{,}5\);
— расстояние — \(6{,}5\) единиц.
г) Точки \(R(-3{,}5)\) и \(Q(0)\)
\[
RQ = \left| -3{,}5 — 0 \right| = \left| -3{,}5 \right| = 3{,}5
\]
На координатной прямой:
— точка \(R\) — в точке \(-3{,}5\);
— точка \(Q\) — в начале координат, \(0\);
— расстояние — \(3{,}5\) единицы.