ГДЗ по Алгебре 7 Класс Номер 6.8 Мордкович — Подробные Ответы

На координатной прямой отмечены точки, соответствующие выражениям. Требуется определить их положение относительно нуля и друг друга, используя свойства чисел и координатной прямой.

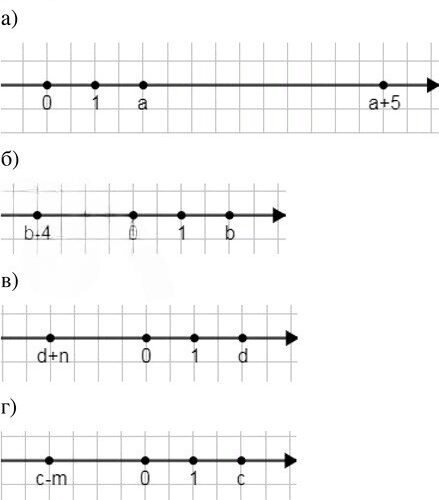
а) На рисунке изображена координатная прямая с точками \(0\), \(1\), \(a\) и \(a+5\).

Из рисунка видно, что:

— \(a > 1\), так как точка \(a\) находится правее точки \(1\);
— \(a + 5 > a\), поскольку прибавление положительного числа (5) сдвигает точку вправо;
— следовательно, \(a + 5\) — самая правая точка на прямой.

Порядок точек слева направо:
\[
0,\quad 1,\quad a,\quad a+5
\]

Таким образом, \(a > 1\), и \(a + 5\) — наибольшее число в этой последовательности.

б) На рисунке изображены точки \(b — 4\), \(0\), \(1\), \(b\).

Из рисунка видно:

— точка \(b\) находится правее \(1\), значит, \(b > 1\);
— точка \(b — 4\) лежит левее нуля, значит, \(b — 4 < 0\);
— тогда \(b < 4\), так как \(b — 4 < 0 \Rightarrow b < 4\).

Следовательно, \(1 < b < 4\).

Порядок точек слева направо:
\[
b — 4,\quad 0,\quad 1,\quad b
\]

Таким образом, \(b — 4 < 0 < 1 < b\).

в) На рисунке изображены точки \(d + n\), \(0\), \(1\), \(d\).

Из рисунка видно:

— точка \(d\) находится правее \(1\), значит, \(d > 1\);
— точка \(d + n\) находится левее нуля, значит, \(d + n < 0\);
— следовательно, \(n < -d\), и так как \(d > 1\), то \(n < -1\).

Порядок точек слева направо:
\[
d + n,\quad 0,\quad 1,\quad d
\]

Значит, \(d + n < 0 < 1 < d\).

г)На рисунке изображены точки \(c — m\), \(0\), \(1\), \(c\).

Из рисунка видно:

— точка \(c\) находится правее \(1\), значит, \(c > 1\);
— точка \(c — m\) находится левее нуля, значит, \(c — m < 0\);
— следовательно, \(m > c\), а так как \(c > 1\), то \(m > 1\).

Порядок точек слева направо:
\[
c — m,\quad 0,\quad 1,\quad c
\]

Значит, \(c — m < 0 < 1 < c\).