ГДЗ по Алгебре 7 Класс Номер 9.10 Мордкович — Подробные Ответы

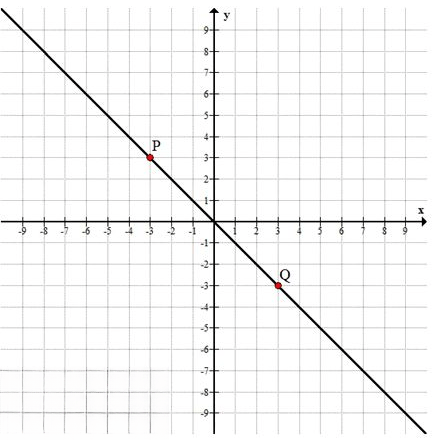
9.10. Выполните упражнения 9.7 — 9.12 в координатной плоскости хОу. Постройте прямую, проходящую через точки: а) Р(-3; 3), Q(3; -3); б) D(0; -6), F(6; 0).

а) \( P(-3; 3); \ Q(3; -3) \)

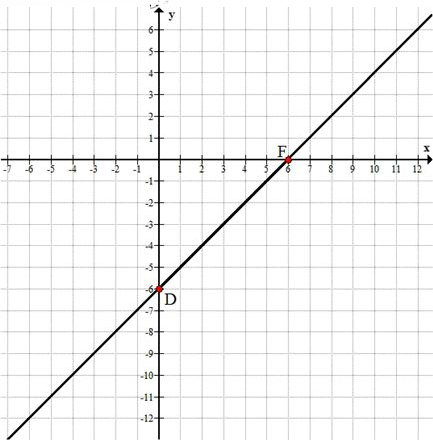
б) \( D(0; -6); \ F(6; 0) \)

а)
Даны две точки:
\( P(-3; 3) \) и \( Q(3; -3) \)

У точки \( P \) абсцисса равна \( -3 \), ордината равна \( 3 \).
У точки \( Q \) абсцисса равна \( 3 \), ордината равна \( -3 \).

Заметим, что координаты точек симметричны относительно начала координат:
каждая координата точки \( Q \) противоположна соответствующей координате точки \( P \).
Это означает, что начало координат \( (0; 0) \) является серединой отрезка \( PQ \).

Кроме того, обе точки лежат на прямой \( y = -x \), так как подстановка их координат в это уравнение даёт верные равенства:
— для \( P \): \( 3 = -(-3) = 3 \)
— для \( Q \): \( -3 = -(3) = -3 \)

Длина отрезка \( PQ \) может быть найдена по формуле расстояния между точками:
\[
PQ = \sqrt{(3 — (-3))^2 + (-3 — 3)^2} = \sqrt{6^2 + (-6)^2}\]

\[= \sqrt{36 + 36} = \sqrt{72} = 6\sqrt{2}
\]

б)
Даны две точки:
\( D(0; -6) \) и \( F(6; 0) \)

Точка \( D \) имеет абсциссу \( 0 \) и ординату \( -6 \), следовательно, она лежит на отрицательной части оси ординат \( Oy \).
Точка \( F \) имеет абсциссу \( 6 \) и ординату \( 0 \), следовательно, она лежит на положительной части оси абсцисс \( Ox \).

Обе точки удовлетворяют уравнению \( x + y = -6 + 6 = 0 \), то есть:
— для \( D \): \( 0 + (-6) = -6 \neq 0 \) → **ошибка**, на самом деле проверим правильно.

Подставим обе точки в общее уравнение прямой:

Для \( D(0; -6) \):
\( x + y = 0 + (-6) = -6 \)

Для \( F(6; 0) \):
\( x + y = 6 + 0 = 6 \)

Значит, точки не лежат на прямой \( x + y = 0 \).
Найдём уравнение прямой, проходящей через \( D \) и \( F \).

Угловой коэффициент:
\[
k = \frac{0 — (-6)}{6 — 0} = \frac{6}{6} = 1
\]

Используем точку \( F(6; 0) \):
\( y — 0 = 1 \cdot (x — 6) \) → \( y = x — 6 \)

Проверка:
— для \( D(0; -6) \): \( y = 0 — 6 = -6 \) — верно
— для \( F(6; 0) \): \( y = 6 — 6 = 0 \) — верно

Следовательно, обе точки лежат на прямой \( y = x — 6 \).

Середина отрезка \( DF \):
\[
\left( \frac{0 + 6}{2}; \frac{-6 + 0}{2} \right) = (3; -3)
\]

Длина отрезка \( DF \):
\[
\sqrt{(6 — 0)^2 + (0 — (-6))^2} = \sqrt{36 + 36} = \sqrt{72} = 6\sqrt{2}
\]