ГДЗ по Алгебре 7 Класс Номер 9.11 Мордкович — Подробные Ответы

Выполните упражнения 9.7 — 9.12 в координатной плоскости хОу. Постройте отрезок \(А_1В_1\), симметричный отрезку АВ относительно начала координат, и найдите координаты его концов, если: а) А(-3; 1), В(—1; 5); б) А(-2; -2), В(1; -4); в) А(—4; 0), В(0; 5); г) А(2; 3), В(-2; -3).

Отрезок \( A_1B_1 \) симметричен отрезку \( AB \) относительно начала координат.

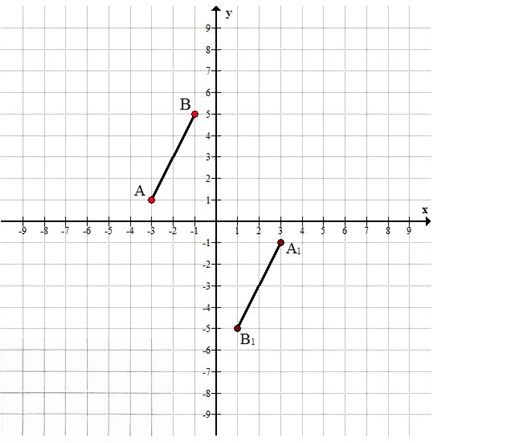
а) \( A(-3; 1), B(-1; 5) \Longrightarrow A_1(3; -1), B_1(1; -5) \)

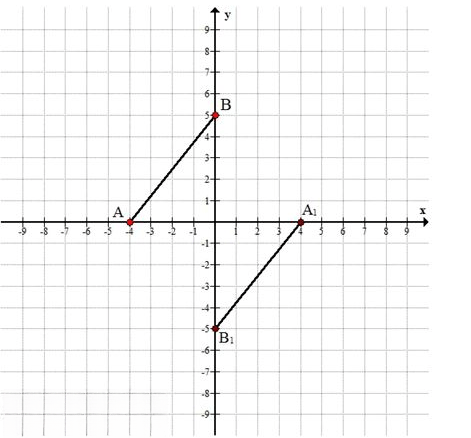
б) \( A(-4; 0), B(0; 5) \Longrightarrow A_1(4; 0), B_1(0; -5) \)

в) \( A(2; 3), B(-2; -3) \Longrightarrow A_1(-2; -3), B_1(2; 3) \)

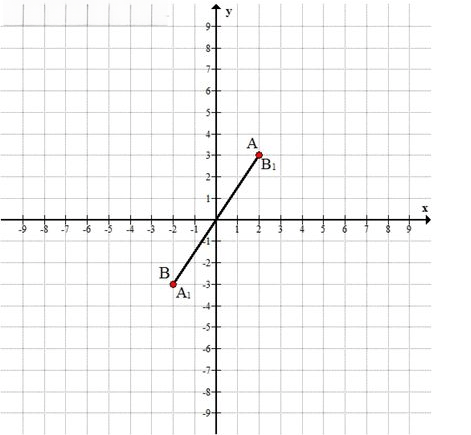
г) \( A(2; 3), B(-2; -3) \Longrightarrow A_1(-2; -3), B_1(2; 3) \)

Отрезок \( A_1B_1 \) симметричен отрезку \( AB \) относительно начала координат.

а)
Даны точки:
\( A(-3; 1) \), \( B(-1; 5) \)

Симметрия относительно начала координат означает, что каждая точка \( (x; y) \) преобразуется в точку \( (-x; -y) \).

Найдём образы:

— Для точки \( A(-3; 1) \):
Заменим \( x = -3 \) на \( -x = 3 \),
заменим \( y = 1 \) на \( -y = -1 \).
Получаем: \( A_1(3; -1) \)

— Для точки \( B(-1; 5) \):
Заменим \( x = -1 \) на \( -x = 1 \),
заменим \( y = 5 \) на \( -y = -5 \).
Получаем: \( B_1(1; -5) \)

Таким образом:
\( A(-3; 1), B(-1; 5) \Longrightarrow A_1(3; -1), B_1(1; -5) \)

На графике это означает, что отрезок \( AB \), расположенный во второй четверти, переходит в отрезок \( A_1B_1 \), расположенный в четвёртой четверти.
Оба отрезка равны по длине и направлены противоположно относительно начала координат.

б)
Даны точки:
\( A(-2; -2) \), \( B(1; -4) \)

Применяем правило симметрии:
Каждую координату меняем знаком.

— Для точки \( A(-2; -2) \):
\( -x = 2 \), \( -y = 2 \) → \( A_1(2; 2) \)

— Для точки \( B(1; -4) \):
\( -x = -1 \), \( -y = 4 \) → \( B_1(-1; 4) \)

Таким образом:
\( A(-2; -2), B(1; -4) \Longrightarrow A_1(2; 2), B_1(-1; 4) \)

Отрезок \( AB \) лежит в третьей и четвёртой четвертях, его образ \( A_1B_1 \) — в первой и второй.
Середина отрезка \( AB \):

\[
\left( \frac{-2 + 1}{2}; \frac{-2 + (-4)}{2} \right) = \left( -\frac{1}{2}; -3 \right)
\]

Середина отрезка \( A_1B_1 \):

\[
\left( \frac{2 + (-1)}{2}; \frac{2 + 4}{2} \right) = \left( \frac{1}{2}; 3 \right)
\]
Эти середины также симметричны относительно начала координат.

в)
Даны точки:
\( A(-4; 0) \), \( B(0; 5) \)

Применяем симметрию:

— Для \( A(-4; 0) \):
\( -x = 4 \), \( -y = 0 \) → \( A_1(4; 0) \)

— Для \( B(0; 5) \):
\( -x = 0 \), \( -y = -5 \) → \( B_1(0; -5) \)

Таким образом:
\( A(-4; 0), B(0; 5) \Longrightarrow A_1(4; 0), B_1(0; -5) \)

На графике:
— Точка \( A \) лежит на отрицательной части оси \( Ox \), её образ — на положительной.
— Точка \( B \) лежит на положительной части оси \( Oy \), её образ — на отрицательной.
Отрезок \( AB \) проходит из четвёртой в первую четверть, а его образ — из первой в четвёртую, но зеркально.

г)
Даны точки:
\( A(2; 3) \), \( B(-2; -3) \)

Применяем симметрию:

— Для \( A(2; 3) \):
\( -x = -2 \), \( -y = -3 \) → \( A_1(-2; -3) \)

— Для \( B(-2; -3) \):
\( -x = 2 \), \( -y = 3 \) → \( B_1(2; 3) \)

Таким образом:
\( A(2; 3), B(-2; -3) \Longrightarrow A_1(-2; -3), B_1(2; 3) \)

Заметим, что:
— \( A_1 \) совпадает с исходной точкой \( B \)
— \( B_1 \) совпадает с исходной точкой \( A \)

Это означает, что точки \( A \) и \( B \) уже симметричны друг другу относительно начала координат.
Поэтому при симметрии отрезок \( AB \) переходит в себя — концы просто меняются местами.

На графике:
Отрезок \( AB \) проходит через начало координат, так как его середина:
\[
\left( \frac{2 + (-2)}{2}; \frac{3 + (-3)}{2} \right) = (0; 0)
\]