Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 9.12 Мордкович — Подробные Ответы
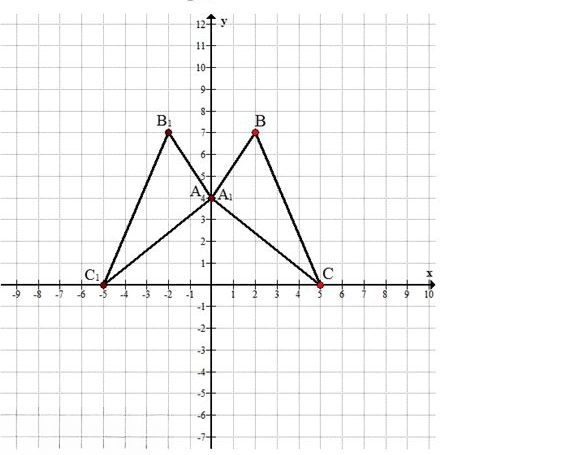
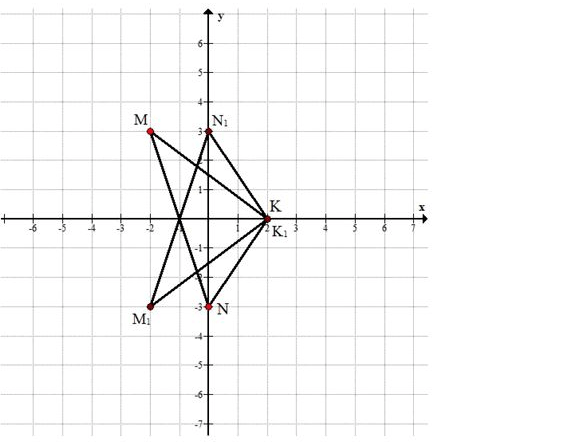
Выполните упражнения 9.7 — 9.12 в координатной плоскости хОу. а) Постройте треугольник \(А_1В_1С_1\), симметричный треугольнику АВС относительно оси ординат, если А(0; 4), В(2; 7), С(5; 0). Найдите координаты вершин треугольника \(А_1В_1С_1\). б) Постройте треугольник \(M_1K_1N_1\), симметричный треугольнику MKN относительно оси абсцисс, если М(-2; 3), К(2; 0), N(0; —3). Найдите координаты вершин треугольника \(M_1K_1N_1\).
а)
\( A(0; 4) \rightarrow A_1(0; 4) \)
\( B(2; 7) \rightarrow B_1(-2; 7) \)
\( C(5; 0) \rightarrow C_1(-5; 0) \)
б)
\( M(-2; 3) \rightarrow M_1(-2; -3) \)
\( K(2; 0) \rightarrow K_1(2; 0) \)
\( N(0; -3) \rightarrow N_1(0; 3) \)
а) Симметрия относительно оси ординат (ось \( y \))
При симметрии относительно оси \( y \) каждая точка \( (x; y) \) переходит в точку \( (-x; y) \).
То есть абсцисса меняет знак на противоположный, а ордината остаётся без изменений.
Рассмотрим вершины исходного треугольника:
— Точка \( A(0; 4) \):
\( x = 0 \rightarrow -x = 0 \), \( y = 4 \)
Следовательно, \( A_1 = (0; 4) \)
(Точка лежит на оси симметрии, поэтому совпадает со своим образом.)
— Точка \( B(2; 7) \):
\( x = 2 \rightarrow -x = -2 \), \( y = 7 \)
Следовательно, \( B_1 = (-2; 7) \)
— Точка \( C(5; 0) \):
\( x = 5 \rightarrow -x = -5 \), \( y = 0 \)
Следовательно, \( C_1 = (-5; 0) \)
Итог:
Треугольник \( A_1B_1C_1 \) с вершинами
\( A_1(0; 4) \), \( B_1(-2; 7) \), \( C_1(-5; 0) \)
является симметричным исходному треугольнику \( ABC \) относительно оси ординат.
б) Симметрия относительно оси абсцисс (ось \( x \))
При симметрии относительно оси \( x \) каждая точка \( (x; y) \) переходит в точку \( (x; -y) \).
То есть ордината меняет знак на противоположный, а абсцисса остаётся без изменений.
Рассмотрим вершины исходного треугольника:
— Точка \( M(-2; 3) \):
\( x = -2 \), \( y = 3 \rightarrow -y = -3 \)
Следовательно, \( M_1 = (-2; -3) \)
— Точка \( K(2; 0) \):
\( x = 2 \), \( y = 0 \rightarrow -y = 0 \)
Следовательно, \( K_1 = (2; 0) \)
(Точка лежит на оси симметрии, поэтому совпадает со своим образом.)
— Точка \( N(0; -3) \):
\( x = 0 \), \( y = -3 \rightarrow -y = 3 \)
Следовательно, \( N_1 = (0; 3) \)
Итог:
Треугольник \( M_1K_1N_1 \) с вершинами
\( M_1(-2; -3) \), \( K_1(2; 0) \), \( N_1(0; 3) \)
является симметричным исходному треугольнику \( MKN \) относительно оси абсцисс.