Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 9.9 Мордкович — Подробные Ответы
Выполните упражнения 9.7 — 9.12 в координатной плоскости хОу. Постройте отрезок MN, если: а) М(-1; 4), N(4; -1); б) М(0; 5), N(5; 0).
а)
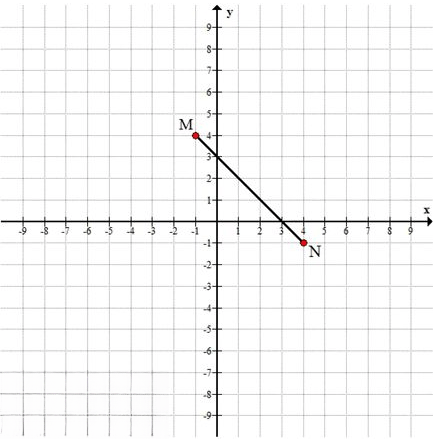
\( M(-1; 4), N(4; -1) \)
б)
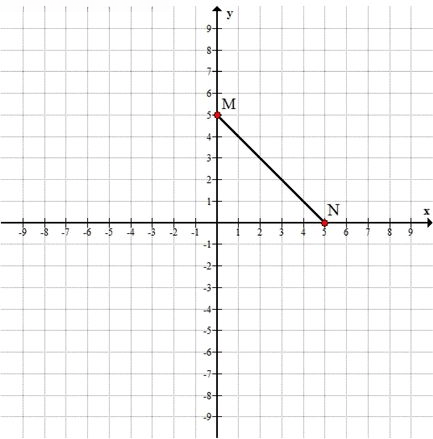
\( M(0; 5), N(5; 0) \)
а)
Даны две точки:
\( M(-1; 4) \) и \( N(4; -1) \)
У точки \( M \) абсцисса равна \( -1 \), ордината равна \( 4 \).
У точки \( N \) абсцисса равна \( 4 \), ордината равна \( -1 \).
Заметим, что координаты точек симметричны относительно прямой \( y = -x \):
абсцисса одной точки равна ординате другой с противоположным знаком, и наоборот.
Эти точки могут быть использованы, например, для построения отрезка \( MN \), нахождения его середины, длины или уравнения прямой, проходящей через них.
б)
Даны две точки:
\( M(0; 5) \) и \( N(5; 0) \)
У точки \( M \) абсцисса равна \( 0 \), ордината равна \( 5 \) — точка лежит на оси \( Oy \).
У точки \( N \) абсцисса равна \( 5 \), ордината равна \( 0 \) — точка лежит на оси \( Ox \).
Обе точки лежат на прямой вида \( x + y = 5 \), так как:
— для \( M \): \( 0 + 5 = 5 \)
— для \( N \): \( 5 + 0 = 5 \)
Отрезок \( MN \) является гипотенузой прямоугольного треугольника с катетами по осям координат, а его длина равна \( \sqrt{(5 — 0)^2 + (0 — 5)^2} = \sqrt{25 + 25} = \sqrt{50} = 5\sqrt{2} \).
Также середина отрезка \( MN \) находится в точке \( \left( \frac{0 + 5}{2}; \frac{5 + 0}{2} \right) = (2{,}5; 2{,}5) \), которая лежит на биссектрисе первого координатного угла \( y = x \).