ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 1 Мордкович — Подробные Ответы

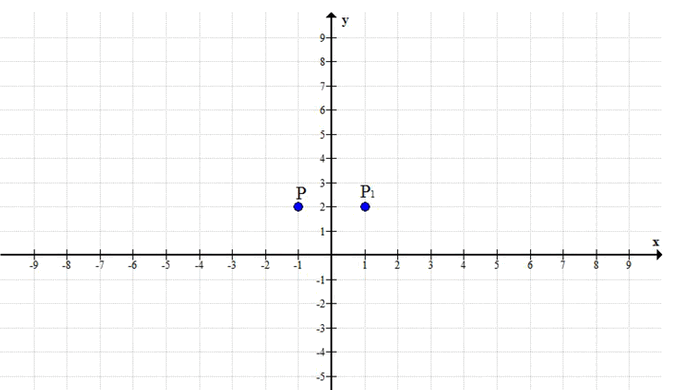
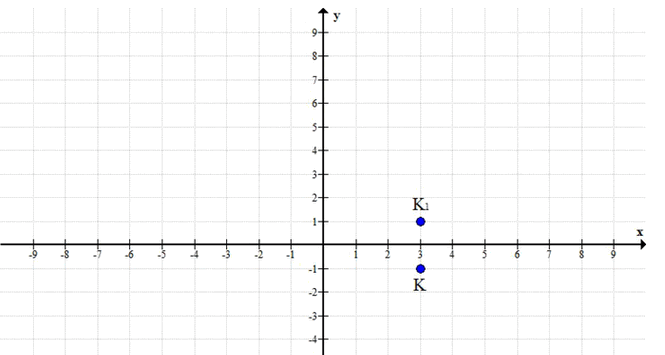
а) Отметьте на координатной плоскости точку Р(—1; 2). Найдите точку, симметричную данной относительно оси ординат. б) Отметьте на координатной плоскости точку К(3; —1). Найдите точку, симметричную данной относительно оси абсцисс.

а)
Пусть точка Р имеет координаты \( (x_1, y_1) = (-1, 2) \).
Точка, симметричная данной относительно оси ординат, имеет координаты \( (-x_1, y_1) \).
Следовательно, координаты симметричной точки равны \( (-(-1), 2) = (1, 2) \).

Ответ: (1; 2)

б)
Пусть точка К имеет координаты \( (x_2, y_2) = (3, -1) \).
Точка, симметричная данной относительно оси абсцисс, имеет координаты \( (x_2, -y_2) \).
Следовательно, координаты симметричной точки равны \( (3, -(-1)) = (3, 1) \).

Ответ: (3; 1)

Условие:

а) Отметить точку Р(-1; 2) и найти симметричную ей относительно оси ординат.

б) Отметить точку К(3; -1) и найти симметричную ей относительно оси абсцисс.

Решение:
а) Точка Р имеет координаты \( (-1; 2) \). Ось ординат — это ось \( y \). При симметрии относительно оси ординат изменяется только знак абсциссы (x-координаты), а ордината (y-координат

а) остается прежней.
Пусть точка, симметричная точке Р относительно оси ординат, имеет координаты \( P'(x’; y’) \).
Тогда \( x’ = -x \) и \( y’ = y \).
Для точки Р(-1; 2):
\( x’ = -(-1) = 1 \)
\( y’ = 2 \)
Следовательно, точка, симметричная точке Р(-1; 2) относительно оси ординат, имеет координаты \( P'(1; 2) \).

б) Точка К имеет координаты \( (3; -1) \). Ось абсцисс — это ось \( x \). При симметрии относительно оси абсцисс изменяется только знак ординаты (y-координаты), а абсцисса (x-координата) остается прежней.
Пусть точка, симметричная точке К относительно оси абсцисс, имеет координаты \( K'(x»; y») \).
Тогда \( x» = x \) и \( y» = -y \).
Для точки К(3; -1):
\( x» = 3 \)
\( y» = -(-1) = 1 \)
Следовательно, точка, симметричная точке К(3; -1) относительно оси абсцисс, имеет координаты \( K»(3; 1) \).

Ответы:

а) P'(1; 2)

б) K»(3; 1)