Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 10 Мордкович — Подробные Ответы
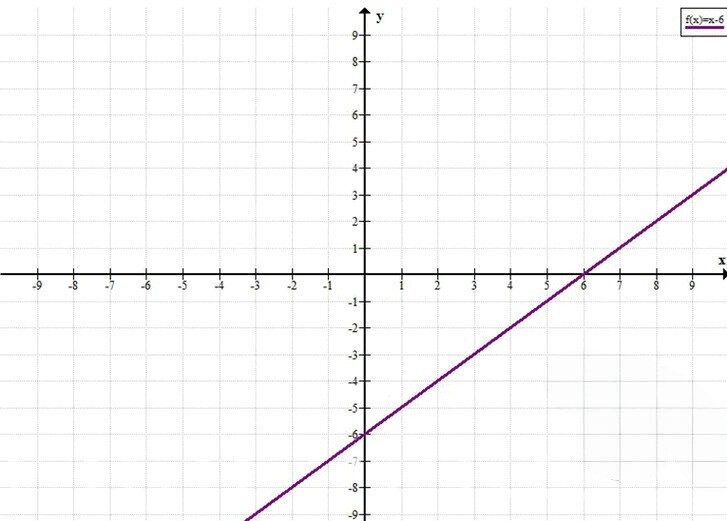
Постройте график функции у = х — 6. По графику найдите: а) значение функции, если значение аргумента равно -2; 0; 3; б) значение аргумента, если значение функции равно —1; 0; 2; в) значения аргумента, при которых у > 0, у < 0; г) наибольшее и наименьшее значения функции на отрезке [1; 3].
а)
\( у = х — 6 \)
Если \( х = -2 \), то \( у = -2 — 6 = -8 \)
Если \( х = 0 \), то \( у = 0 — 6 = -6 \)
Если \( х = 3 \), то \( у = 3 — 6 = -3 \)
Ответ: -8; -6; -3
б)
\( у = х — 6 \)
Если \( у = -1 \), то \( -1 = х — 6 \), \( х = -1 + 6 = 5 \)
Если \( у = 0 \), то \( 0 = х — 6 \), \( х = 6 \)
Если \( у = 2 \), то \( 2 = х — 6 \), \( х = 2 + 6 = 8 \)
Ответ: 5; 6; 8
в)
\( у > 0 \)
\( х — 6 > 0 \)
\( х > 6 \)
\( у < 0 \)
\( х — 6 < 0 \)
\( х < 6 \)
Ответ: \( х > 6 \); \( х < 6 \)
г)
На отрезке [1; 3] функция \( у = х — 6 \) является возрастающей.
Наименьшее значение достигается при \( х = 1 \): \( у = 1 — 6 = -5 \)
Наибольшее значение достигается при \( х = 3 \): \( у = 3 — 6 = -3 \)
Ответ: Наибольшее значение -3, наименьшее значение -5
Условие: Построить график функции \(у = х — 6\) и найти по графику:
а) значение функции при \(х = -2, 0, 3\);
б) значение аргумента при \(у = -1, 0, 2\);
в) значения аргумента, при которых \(у > 0, у < 0\);
г) наибольшее и наименьшее значения функции на отрезке [1; 3].
Решение:
Для построения графика функции \(у = х — 6\) найдем две точки.
При \(х = 0\), \(у = 0 — 6 = -6\). Точка (0; -6).
При \(у = 0\), \(0 = х — 6\), \(х = 6\). Точка (6; 0).
Построим прямую, проходящую через точки (0; -6) и (6; 0).
а) По графику найдем значение функции, если значение аргумента равно -2; 0; 3.
Если \(х = -2\), то \(у = -2 — 6 = -8\).
Если \(х = 0\), то \(у = 0 — 6 = -6\).
Если \(х = 3\), то \(у = 3 — 6 = -3\).
б) По графику найдем значение аргумента, если значение функции равно —1; 0; 2.
Если \(у = -1\), то \(-1 = х — 6\), \(х = -1 + 6 = 5\).
Если \(у = 0\), то \(0 = х — 6\), \(х = 6\).
Если \(у = 2\), то \(2 = х — 6\), \(х = 2 + 6 = 8\).
в) По графику найдем значения аргумента, при которых \(у > 0\) и \(у < 0\).
\(у > 0\) когда прямая находится выше оси абсцисс. Это происходит при \(х > 6\).
\(у < 0\) когда прямая находится ниже оси абсцисс. Это происходит при \(х < 6\).
г) По графику найдем наибольшее и наименьшее значения функции на отрезке [1; 3].
Функция \(у = х — 6\) является возрастающей.
На отрезке [1; 3] наименьшее значение будет при \(х = 1\): \(у = 1 — 6 = -5\).
На отрезке [1; 3] наибольшее значение будет при \(х = 3\): \(у = 3 — 6 = -3\).
Ответы:
а) При \(х = -2\), \(у = -8\); при \(х = 0\), \(у = -6\); при \(х = 3\), \(у = -3\).
б) При \(у = -1\), \(х = 5\); при \(у = 0\), \(х = 6\); при \(у = 2\), \(х = 8\).
в) \(у > 0\) при \(х > 6\); \(у < 0\) при \(х < 6\).
г) Наименьшее значение функции на отрезке [1; 3] равно -5, наибольшее значение равно -3.