ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 11 Мордкович — Подробные Ответы

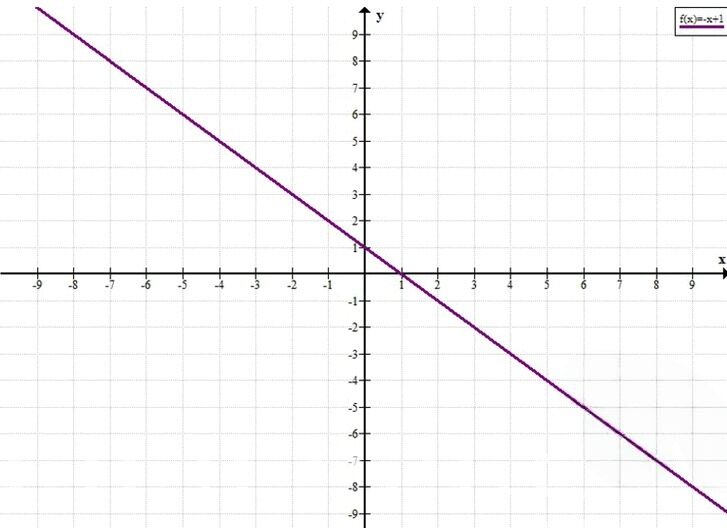
Постройте график функции у = -х + 1. По графику найдите: а) значение функции, если значение аргумента равно -3; 0; 2; б) значение аргумента, если значение функции равно -2; 0; 1; в) значения аргумента, при которых у > 0, у < 0; г) наибольшее и наименьшее значения функции на отрезке [-2; 1].

Для построения графика функции \(y = -x + 1\) найдем несколько точек:
Если \(x = -2\), то \(y = -(-2) + 1 = 3\). Точка \((-2; 3)\).
Если \(x = 0\), то \(y = -(0) + 1 = 1\). Точка \((0; 1)\).
Если \(x = 1\), то \(y = -(1) + 1 = 0\). Точка \((1; 0)\).
Если \(x = 2\), то \(y = -(2) + 1 = -1\). Точка \((2; -1)\).

а) Найдем значение функции, если значение аргумента равно -3; 0; 2:
Если \(x = -3\):
\(y = -(-3) + 1\)
\(y = 3 + 1\)
\(y = 4\)

Если \(x = 0\):
\(y = -(0) + 1\)
\(y = 0 + 1\)
\(y = 1\)

Если \(x = 2\):
\(y = -(2) + 1\)
\(y = -2 + 1\)
\(y = -1\)
Ответ: 4; 1; -1

б) Найдем значение аргумента, если значение функции равно -2; 0; 1:
Если \(y = -2\):
\(-2 = -x + 1\)
\(-x = -2 — 1\)
\(-x = -3\)
\(x = 3\)

Если \(y = 0\):
\(0 = -x + 1\)
\(-x = -1\)
\(x = 1\)

Если \(y = 1\):
\(1 = -x + 1\)
\(-x = 1 — 1\)
\(-x = 0\)
\(x = 0\)
Ответ: 3; 1; 0

в) Найдем значения аргумента, при которых \(y > 0\), \(y < 0\):
При \(y > 0\):
\(-x + 1 > 0\)
\(-x > -1\)
\(x < 1\)

При \(y < 0\):
\(-x + 1 < 0\)
\(-x < -1\)
\(x > 1\)
Ответ: при \(x < 1\), \(y > 0\); при \(x > 1\), \(y < 0\)

г) Найдем наибольшее и наименьшее значения функции на отрезке \([-2; 1]\):
Функция \(y = -x + 1\) является убывающей, так как коэффициент при \(x\) отрицательный.
Наибольшее значение функции на отрезке достигается в левой границе отрезка, то есть при \(x = -2\):
\(y = -(-2) + 1\)
\(y = 2 + 1\)
\(y = 3\)

Наименьшее значение функции на отрезке достигается в правой границе отрезка, то есть при \(x = 1\):
\(y = -(1) + 1\)
\(y = -1 + 1\)
\(y = 0\)
Ответ: наибольшее значение 3, наименьшее значение 0

Условие: Построить график функции \(у = -х + 1\) и по графику найти:

а) значение функции, если значение аргумента равно -3; 0; 2;

б) значение аргумента, если значение функции равно -2; 0; 1;

в) значения аргумента, при которых \(у > 0, у < 0\);

г) наибольшее и наименьшее значения функции на отрезке \([-2; 1]\).

Решение:
1. Построим график функции \(у = -х + 1\).
Это линейная функция, графиком которой является прямая. Для построения прямой достаточно двух точек.
Найдем координаты двух точек:
Если \(х = 0\), то \(у = -0 + 1 = 1\). Получаем точку \((0; 1)\).
Если \(х = 1\), то \(у = -1 + 1 = 0\). Получаем точку \((1; 0)\).
Отметим эти точки на координатной плоскости и проведем через них прямую.

2. Найдем значения по графику (или путем подстановки в уравнение функции, что эквивалентно чтению с графика):

а) Значение функции, если значение аргумента равно -3; 0; 2.
При \(х = -3\):
\(у = -(-3) + 1\)
\(у = 3 + 1\)
\(у = 4\).
При \(х = 0\):
\(у = -0 + 1\)
\(у = 1\).
При \(х = 2\):
\(у = -2 + 1\)
\(у = -1\).

б) Значение аргумента, если значение функции равно -2; 0; 1.
При \(у = -2\):
\(-2 = -х + 1\)
\(х = 1 + 2\)
\(х = 3\).
При \(у = 0\):
\(0 = -х + 1\)
\(х = 1\).
При \(у = 1\):
\(1 = -х + 1\)
\(х = 1 — 1\)
\(х = 0\).

в) Значения аргумента, при которых \(у > 0, у < 0\).
Для \(у > 0\):
\(-х + 1 > 0\)
\(1 > х\)
\(х < 1\).
Для \(у < 0\):
\(-х + 1 < 0\)
\(1 < х\)
\(х > 1\).

г) Наибольшее и наименьшее значения функции на отрезке \([-2; 1]\).
Функция \(у = -х + 1\) является убывающей, так как коэффициент при \(х\) отрицательный \((k = -1)\).
Наибольшее значение убывающая функция принимает на левом конце отрезка.
При \(х = -2\):
\(у_{наиб} = -(-2) + 1\)
\(у_{наиб} = 2 + 1\)
\(у_{наиб} = 3\).
Наименьшее значение убывающая функция принимает на правом конце отрезка.
При \(х = 1\):
\(у_{наим} = -1 + 1\)
\(у_{наим} = 0\).

Ответы:

а) При \(х = -3\), \(у = 4\); при \(х = 0\), \(у = 1\); при \(х = 2\), \(у = -1\).

б) При \(у = -2\), \(х = 3\); при \(у = 0\), \(х = 1\); при \(у = 1\), \(х = 0\).

в) \(у > 0\) при \(х < 1\); \(у < 0\) при \(х > 1\).

г) Наибольшее значение \(3\), наименьшее значение \(0\).