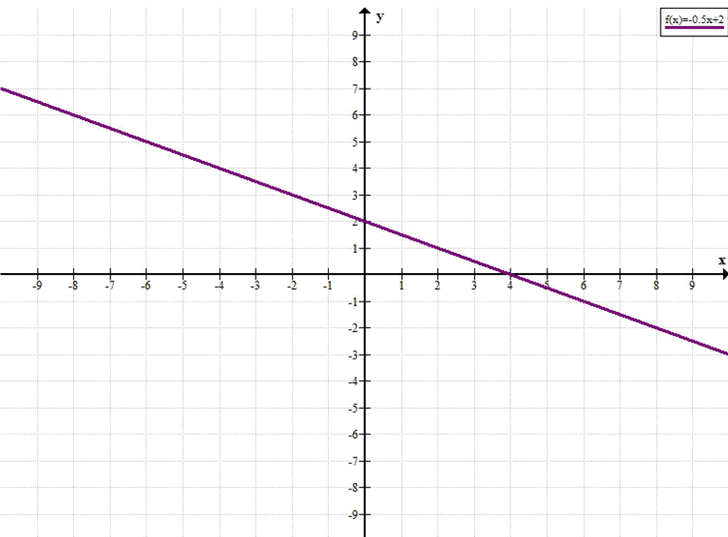ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 13 Мордкович — Подробные Ответы

Постройте график функции у = -0,5x + 2. С помощью графика найдите: а) координаты точек пересечения прямой с осью х и осью у, б) значения аргумента, при которых у > 0, у < 0; в) значения у, которые соответствуют значениям х, удовлетворяющим неравенству -2 < х < 2; г) промежуток, которому принадлежит переменная х, если \(Унаиб = -1. Унаиб = 4.\)

Для построения графика функции \( y = -0,5x + 2 \) достаточно найти две точки.
Например, точки пересечения с осями координат:
При \( x = 0 \), \( y = -0,5 \cdot 0 + 2 = 2 \). Точка \( (0, 2) \).
При \( y = 0 \), \( 0 = -0,5x + 2 \), \( 0,5x = 2 \), \( x = 4 \). Точка \( (4, 0) \).
График функции — прямая, проходящая через точки \( (0, 2) \) и \( (4, 0) \).

а) координаты точек пересечения прямой с осью х и осью у
Пересечение с осью х (когда \( y = 0 \)):
\( 0 = -0,5x + 2 \)
\( 0,5x = 2 \)
\( x = \frac{2}{0,5} \)
\( x = 4 \)
Точка пересечения с осью х: \( (4, 0) \)

Пересечение с осью у (когда \( x = 0 \)):
\( y = -0,5 \cdot 0 + 2 \)
\( y = 2 \)
Точка пересечения с осью у: \( (0, 2) \)

б) значения аргумента, при которых \( y > 0 \), \( y < 0 \)
Для \( y > 0 \):
\( -0,5x + 2 > 0 \)
\( -0,5x > -2 \)
\( x < \frac{-2}{-0,5} \)
\( x < 4 \)

Для \( y < 0 \):
\( -0,5x + 2 < 0 \)
\( -0,5x < -2 \)
\( x > \frac{-2}{-0,5} \)
\( x > 4 \)

в) значения у, которые соответствуют значениям х, удовлетворяющим неравенству \( -2 < x < 2 \)
Функция \( y = -0,5x + 2 \) является убывающей, так как коэффициент при \( x \) отрицательный \( (-0,5 < 0) \).
Найдем значения \( y \) на концах интервала для \( x \):
При \( x = -2 \):
\( y = -0,5(-2) + 2 \)
\( y = 1 + 2 \)
\( y = 3 \)
При \( x = 2 \):
\( y = -0,5(2) + 2 \)
\( y = -1 + 2 \)
\( y = 1 \)
Поскольку функция убывает, то для \( -2 < x < 2 \) значения \( y \) будут находиться в интервале \( (1, 3) \).
То есть \( 1 < y < 3 \).

г) промежуток, которому принадлежит переменная х, если \( Унаиб = -1. Унаиб = 4. \)
Предположим, что это означает, что \( y \) находится в диапазоне от \( -1 \) до \( 4 \), то есть \( -1 \le y \le 4 \).
Найдем значения \( x \), соответствующие этим значениям \( y \).
При \( y = -1 \):
\( -1 = -0,5x + 2 \)
\( -1 — 2 = -0,5x \)
\( -3 = -0,5x \)
\( x = \frac{-3}{-0,5} \)
\( x = 6 \)
При \( y = 4 \):
\( 4 = -0,5x + 2 \)
\( 4 — 2 = -0,5x \)
\( 2 = -0,5x \)
\( x = \frac{2}{-0,5} \)
\( x = -4 \)
Поскольку функция убывающая, то при увеличении \( y \) от \( -1 \) до \( 4 \), значение \( x \) будет уменьшаться от \( 6 \) до \( -4 \).
Следовательно, \( -4 \le x \le 6 \).

Ответы:
а) Точка пересечения с осью х: \( (4, 0) \); Точка пересечения с осью у: \( (0, 2) \)
б)
\( y > 0 \) при \( x < 4 \); \( y < 0 \) при \( x > 4 \)
в)
\( 1 < y < 3 \)
г)
\( -4 \le x \le 6 \)

Условие: Постройте график функции \(у = -0,5x + 2\). С помощью графика найдите:

а) координаты точек пересечения прямой с осью х и осью у,

б) значения аргумента, при которых \(у > 0, у < 0\);

в) значения \(у\), которые соответствуют значениям \(х\), удовлетворяющим неравенству \(-2 < х < 2\); г) промежуток, которому принадлежит переменная \(х\), если \(-1 \le у \le 4\).

Решение:
1. Построение графика функции \(у = -0,5x + 2\).
Функция \(у = -0,5x + 2\) является линейной, её графиком является прямая. Для построения прямой достаточно найти две точки.
Найдем точки пересечения с осями координат.
При \(x = 0\):
\(у = -0,5 \cdot 0 + 2\)
\(у = 2\)
Первая точка: \((0, 2)\).
При \(у = 0\):
\(0 = -0,5x + 2\)
\(0,5x = 2\)
\(x = 2 / 0,5\)
\(x = 4\)
Вторая точка: \((4, 0)\).
Для построения графика необходимо отметить точки \((0, 2)\) и \((4, 0)\) на координатной плоскости и провести через них прямую.

2. Нахождение свойств функции с помощью графика.

а) Координаты точек пересечения прямой с осью х и осью у.
Из построения графика видно, что прямая пересекает ось \(х\) в точке \((4, 0)\).
Прямая пересекает ось \(у\) в точке \((0, 2)\).

б) Значения аргумента, при которых \(у > 0, у < 0\).
График функции находится выше оси \(х\) (то есть \(у > 0\)) при значениях \(х\), меньших координаты точки пересечения с осью \(х\).
Следовательно, \(у > 0\) при \(x < 4\).
График функции находится ниже оси \(х\) (то есть \(у < 0\)) при значениях \(х\), больших координаты точки пересечения с осью \(х\).
Следовательно, \(у < 0\) при \(x > 4\).

в) Значения \(у\), которые соответствуют значениям \(х\), удовлетворяющим неравенству \(-2 < х < 2\).
Найдем значения \(у\) на концах интервала для \(х\).
При \(x = -2\):
\(у = -0,5 \cdot (-2) + 2\)
\(у = 1 + 2\)
\(у = 3\)
При \(x = 2\):
\(у = -0,5 \cdot 2 + 2\)
\(у = -1 + 2\)
\(у = 1\)
Поскольку функция \(у = -0,5x + 2\) является убывающей (коэффициент при \(х\) отрицательный), то при увеличении \(х\) значение \(у\) уменьшается.
Следовательно, для \(-2 < х < 2\) значения \(у\) будут находиться в промежутке между \(1\) и \(3\).
То есть, \(1 < у < 3\).

г) Промежуток, которому принадлежит переменная \(х\), если \(-1 \le у \le 4\).
Найдем значения \(х\), при которых \(у = -1\) и \(у = 4\).
При \(у = -1\):
\(-1 = -0,5x + 2\)
\(-0,5x = -1 — 2\)
\(-0,5x = -3\)
\(x = -3 / (-0,5)\)
\(x = 6\)
При \(у = 4\):
\(4 = -0,5x + 2\)
\(-0,5x = 4 — 2\)
\(-0,5x = 2\)
\(x = 2 / (-0,5)\)
\(x = -4\)
Поскольку функция убывающая, то если \(у\) находится в промежутке от \(-1\) до \(4\), то \(х\) будет находиться в промежутке от \(-4\) до \(6\).
То есть, \(-4 \le x \le 6\).

Ответы:
а) Точки пересечения: с осью \(х\) — \((4, 0)\), с осью \(у\) — \((0, 2)\).
б)
\(у > 0\) при \(x < 4\); \(у < 0\) при \(x > 4\).
в)
\(1 < у < 3\).
г)
\(-4 \le x \le 6\).