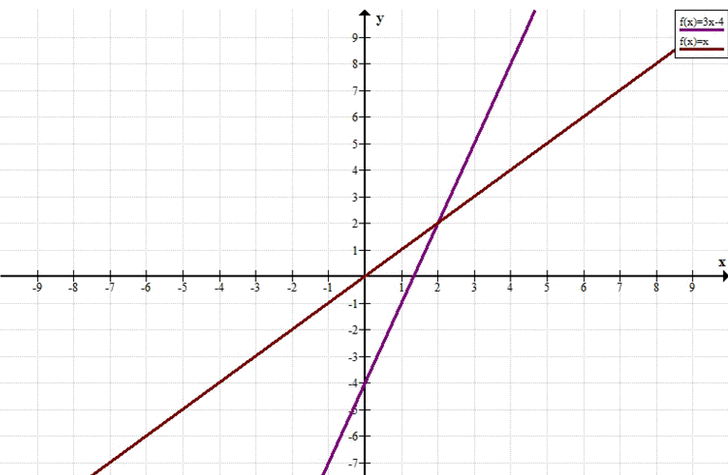ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 17 Мордкович — Подробные Ответы

Найдите точку пересечения прямых графическим и аналитическим методами: а) у = 3х — 4 и у = х; б) у = 1x:3 -3 y= -x + 1; в) у = -2х и у = 0,5х + 5; г) у = -5х — 2 и у = х + 4.

а)
Аналитический метод:
\( 3x — 4 = x \)
\( 3x — x = 4 \)
\( 2x = 4 \)
\( x = 2 \)
\( y = x \)
\( y = 2 \)
Точка пересечения: \( (2; 2) \)

Графический метод:
Построим график функции \( y = 3x — 4 \):
При \( x = 0 \), \( y = -4 \). Точка \( (0; -4) \).
При \( x = 2 \), \( y = 3 \cdot 2 — 4 = 6 — 4 = 2 \). Точка \( (2; 2) \).
Построим график функции \( y = x \):
При \( x = 0 \), \( y = 0 \). Точка \( (0; 0) \).
При \( x = 2 \), \( y = 2 \). Точка \( (2; 2) \).
Прямые пересекаются в точке \( (2; 2) \).

Ответ: \( (2; 2) \)

б)
Аналитический метод:
\( \frac{1}{3}x — 3 = -x + 1 \)
\( x — 9 = -3x + 3 \)
\( x + 3x = 3 + 9 \)
\( 4x = 12 \)
\( x = 3 \)
\( y = -x + 1 \)
\( y = -3 + 1 \)
\( y = -2 \)
Точка пересечения: \( (3; -2) \)

Графический метод:
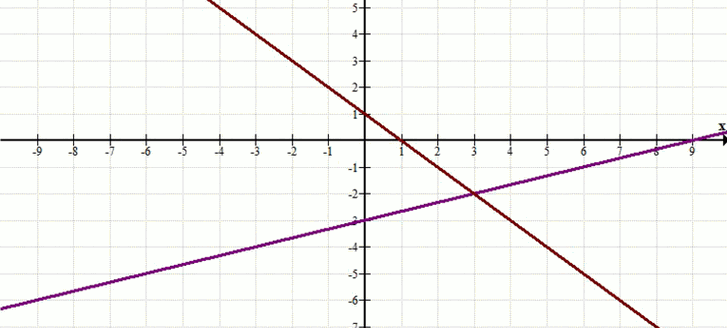
Построим график функции \( y = \frac{1}{3}x — 3 \):
При \( x = 0 \), \( y = -3 \). Точка \( (0; -3) \).
При \( x = 3 \), \( y = \frac{1}{3} \cdot 3 — 3 = 1 — 3 = -2 \). Точка \( (3; -2) \).
Построим график функции \( y = -x + 1 \):
При \( x = 0 \), \( y = 1 \). Точка \( (0; 1) \).
При \( x = 3 \), \( y = -3 + 1 = -2 \). Точка \( (3; -2) \).
Прямые пересекаются в точке \( (3; -2) \).

Ответ: \( (3; -2) \)

в)
Аналитический метод:
\( -2x = 0,5x + 5 \)
\( -2x — 0,5x = 5 \)
\( -2,5x = 5 \)
\( x = \frac{5}{-2,5} \)
\( x = -2 \)
\( y = -2x \)
\( y = -2 \cdot (-2) \)
\( y = 4 \)

Точка пересечения: \( (-2; 4) \)

Графический метод:
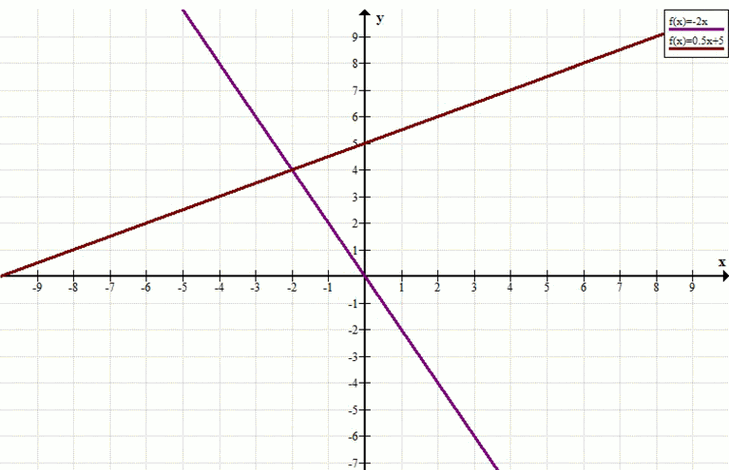
Построим график функции \( y = -2x \):
При \( x = 0 \), \( y = 0 \). Точка \( (0; 0) \).
При \( x = -2 \), \( y = -2 \cdot (-2) = 4 \). Точка \( (-2; 4) \).
Построим график функции \( y = 0,5x + 5 \):
При \( x = 0 \), \( y = 5 \). Точка \( (0; 5) \).
При \( x = -2 \), \( y = 0,5 \cdot (-2) + 5 = -1 + 5 = 4 \). Точка \( (-2; 4) \).
Прямые пересекаются в точке \( (-2; 4) \).

Ответ: \( (-2; 4) \)

г)
Аналитический метод:
\( -5x — 2 = x + 4 \)
\( -5x — x = 4 + 2 \)
\( -6x = 6 \)
\( x = \frac{6}{-6} \)
\( x = -1 \)
\( y = x + 4 \)
\( y = -1 + 4 \)
\( y = 3 \)
Точка пересечения: \( (-1; 3) \)

Графический метод:
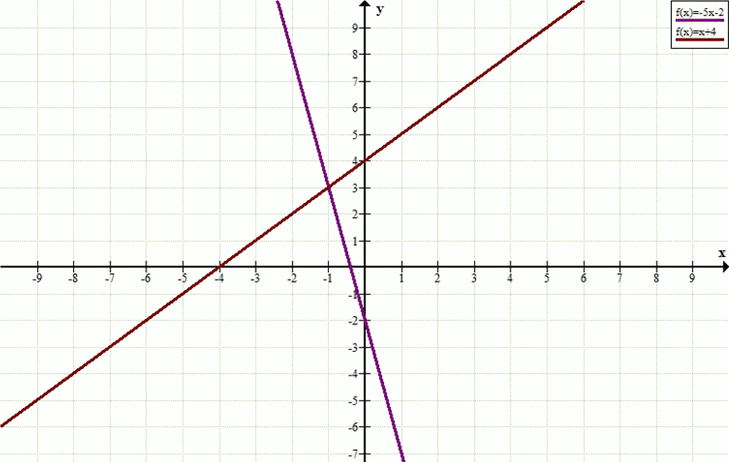
Построим график функции \( y = -5x — 2 \):
При \( x = 0 \), \( y = -2 \). Точка \( (0; -2) \).
При \( x = -1 \), \( y = -5 \cdot (-1) — 2 = 5 — 2 = 3 \). Точка \( (-1; 3) \).
Построим график функции \( y = x + 4 \):
При \( x = 0 \), \( y = 4 \). Точка \( (0; 4) \).
При \( x = -1 \), \( y = -1 + 4 = 3 \). Точка \( (-1; 3) \).
Прямые пересекаются в точке \( (-1; 3) \).

Ответ: \( (-1; 3) \)

Условие: Найдите точку пересечения прямых графическим и аналитическим методами:
а)
\(у = 3х — 4\) и \(у = х\)
б)
\(у = \frac{1}{3}х — 3\) и \(у = -х + 1\)
в)
\(у = -2х\) и \(у = 0,5х + 5\)
г)
\(у = -5х — 2\) и \(у = х + 4\)

Решение:

а) Точка пересечения прямых \(у = 3х — 4\) и \(у = х\)

Графический метод:
Для нахождения точки пересечения графическим методом необходимо построить графики обеих функций в одной координатной плоскости.
График функции \(у = 3х — 4\) является прямой. Для ее построения можно найти две точки, например:
Если \(х = 0\), то \(у = 3 \cdot 0 — 4 = -4\). Точка \((0; -4)\).
Если \(х = 2\), то \(у = 3 \cdot 2 — 4 = 2\). Точка \((2; 2)\).
График функции \(у = х\) является прямой, проходящей через начало координат. Для ее построения можно найти две точки, например:
Если \(х = 0\), то \(у = 0\). Точка \((0; 0)\).
Если \(х = 2\), то \(у = 2\). Точка \((2; 2)\).
Точка пересечения графиков будет иметь координаты, которые удовлетворяют обоим уравнениям.

Аналитический метод:
Для нахождения точки пересечения аналитическим методом приравняем правые части уравнений:
\(3х — 4 = х\)
Перенесем \(х\) в левую часть, а число в правую:
\(3х — х = 4\)
Приведем подобные слагаемые:
\(2х = 4\)
Разделим обе части на 2:
\(х = 4 / 2\)
\(х = 2\)
Теперь подставим найденное значение \(х\) в одно из исходных уравнений, например, в \(у = х\):
\(у = 2\)
Таким образом, точка пересечения имеет координаты \((2; 2)\).

Ответ: \((2; 2)\)

б) Точка пересечения прямых \(у = \frac{1}{3}х — 3\) и \(у = -х + 1\)

Графический метод:
Для нахождения точки пересечения графическим методом необходимо построить графики обеих функций в одной координатной плоскости.
График функции \(у = \frac{1}{3}х — 3\) является прямой. Для ее построения можно найти две точки, например:
Если \(х = 0\), то \(у = \frac{1}{3} \cdot 0 — 3 = -3\). Точка \((0; -3)\).
Если \(х = 3\), то \(у = \frac{1}{3} \cdot 3 — 3 = 1 — 3 = -2\). Точка \((3; -2)\).
График функции \(у = -х + 1\) является прямой. Для ее построения можно найти две точки, например:
Если \(х = 0\), то \(у = -0 + 1 = 1\). Точка \((0; 1)\).
Если \(х = 1\), то \(у = -1 + 1 = 0\). Точка \((1; 0)\).
Точка пересечения графиков будет иметь координаты, которые удовлетворяют обоим уравнениям.

Аналитический метод:
Для нахождения точки пересечения аналитическим методом приравняем правые части уравнений:
\(\frac{1}{3}х — 3 = -х + 1\)
Перенесем слагаемые с \(х\) в левую часть, а числа в правую:
\(\frac{1}{3}х + х = 1 + 3\)
Приведем подобные слагаемые:
\(\frac{1}{3}х + \frac{3}{3}х = 4\)
\(\frac{4}{3}х = 4\)
Умножим обе части на \(\frac{3}{4}\):
\(х = 4 \cdot \frac{3}{4}\)
\(х = 3\)
Теперь подставим найденное значение \(х\) в одно из исходных уравнений, например, в \(у = -х + 1\):
\(у = -3 + 1\)
\(у = -2\)
Таким образом, точка пересечения имеет координаты \((3; -2)\).

Ответ: \((3; -2)\)

в) Точка пересечения прямых \(у = -2х\) и \(у = 0,5х + 5\)

Графический метод:
Для нахождения точки пересечения графическим методом необходимо построить графики обеих функций в одной координатной плоскости.
График функции \(у = -2х\) является прямой, проходящей через начало координат. Для ее построения можно найти две точки, например:
Если \(х = 0\), то \(у = -2 \cdot 0 = 0\). Точка \((0; 0)\).
Если \(х = -2\), то \(у = -2 \cdot (-2) = 4\). Точка \((-2; 4)\).
График функции \(у = 0,5х + 5\) является прямой. Для ее построения можно найти две точки, например:
Если \(х = 0\), то \(у = 0,5 \cdot 0 + 5 = 5\). Точка \((0; 5)\).
Если \(х = -2\), то \(у = 0,5 \cdot (-2) + 5 = -1 + 5 = 4\). Точка \((-2; 4)\).
Точка пересечения графиков будет иметь координаты, которые удовлетворяют обоим уравнениям.

Аналитический метод:
Для нахождения точки пересечения аналитическим методом приравняем правые части уравнений:
\(-2х = 0,5х + 5\)
Перенесем слагаемые с \(х\) в левую часть, а числа в правую:
\(-2х — 0,5х = 5\)
Приведем подобные слагаемые:
\(-2,5х = 5\)
Разделим обе части на \(-2,5\):
\(х = 5 / (-2,5)\)
\(х = -2\)
Теперь подставим найденное значение \(х\) в одно из исходных уравнений, например, в \(у = -2х\):
\(у = -2 \cdot (-2)\)
\(у = 4\)
Таким образом, точка пересечения имеет координаты \((-2; 4)\).

Ответ: \((-2; 4)\)

г) Точка пересечения прямых \(у = -5х — 2\) и \(у = х + 4\)

Графический метод:
Для нахождения точки пересечения графическим методом необходимо построить графики обеих функций в одной координатной плоскости.
График функции \(у = -5х — 2\) является прямой. Для ее построения можно найти две точки, например:
Если \(х = 0\), то \(у = -5 \cdot 0 — 2 = -2\). Точка \((0; -2)\).
Если \(х = -1\), то \(у = -5 \cdot (-1) — 2 = 5 — 2 = 3\). Точка \((-1; 3)\).
График функции \(у = х + 4\) является прямой. Для ее построения можно найти две точки, например:
Если \(х = 0\), то \(у = 0 + 4 = 4\). Точка \((0; 4)\).
Если \(х = -1\), то \(у = -1 + 4 = 3\). Точка \((-1; 3)\).
Точка пересечения графиков будет иметь координаты, которые удовлетворяют обоим уравнениям.

Аналитический метод:
Для нахождения точки пересечения аналитическим методом приравняем правые части уравнений:
\(-5х — 2 = х + 4\)
Перенесем слагаемые с \(х\) в левую часть, а числа в правую:
\(-5х — х = 4 + 2\)
Приведем подобные слагаемые:
\(-6х = 6\)
Разделим обе части на \(-6\):
\(х = 6 / (-6)\)
\(х = -1\)
Теперь подставим найденное значение \(х\) в одно из исходных уравнений, например, в \(у = х + 4\):
\(у = -1 + 4\)
\(у = 3\)
Таким образом, точка пересечения имеет координаты \((-1; 3)\).

Ответ: \((-1; 3)\)