Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 2 Мордкович — Подробные Ответы
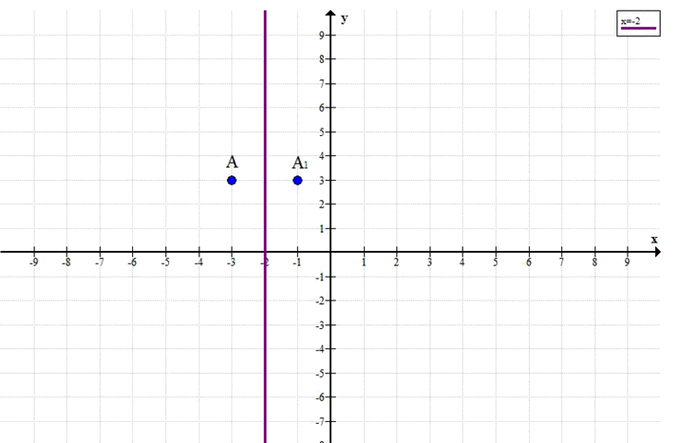
а) Изобразите на координатной плоскости точку А(-3; 3) и прямую х = -2. Найдите точку, симметричную данной относительно построенной прямой, б)Изобразите на координатной плоскости точку С(4; -2) и прямую у = 1. Найдите точку, симметричную данной относительно построенной прямой.
а)
Пусть точка А имеет координаты \( (x_A, y_A) = (-3, 3) \).
Прямая задана уравнением \( x = -2 \).
Точка, симметричная точке А относительно прямой \( x = c \), имеет координаты \( (2c — x_A, y_A) \).
В данном случае \( c = -2 \).
Координата x симметричной точки: \( 2(-2) — (-3) = -4 + 3 = -1 \).
Координата y симметричной точки: \( 3 \).
Симметричная точка А’ имеет координаты \( (-1, 3) \).
Ответ: (-1; 3)
б)
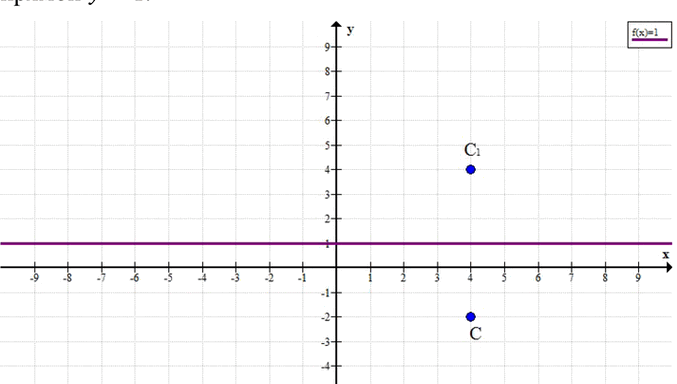
Пусть точка С имеет координаты \( (x_C, y_C) = (4, -2) \).
Прямая задана уравнением \( y = 1 \).
Точка, симметричная точке С относительно прямой \( y = d \), имеет координаты \( (x_C, 2d — y_C) \).
В данном случае \( d = 1 \).
Координата x симметричной точки: \( 4 \).
Координата y симметричной точки: \( 2(1) — (-2) = 2 + 2 = 4 \).
Симметричная точка С’ имеет координаты \( (4, 4) \).
Ответ: (4; 4)
Условие: Найти точки, симметричные заданным относительно прямых.
Решение:
а) Точка А(-3; 3), прямая \(х = -2\).
Симметричная точка А’ будет иметь ту же ординату, что и А, то есть \(y_{A’} = y_A = 3\).
Абсцисса точки А’ будет находиться на таком же расстоянии от прямой \(х = -2\), как и абсцисса точки А, но с другой стороны.
Расстояние от А до прямой \(х = -2\) равно \(|-3 — (-2)| = |-3 + 2| = |-1| = 1\).
Следовательно, абсцисса точки А’ будет \(x_{A’} = -2 + 1 = -1\).
Таким образом, точка, симметричная А(-3; 3) относительно прямой \(х = -2\), имеет координаты А'(-1; 3).
б) Точка С(4; -2), прямая \(у = 1\).
Симметричная точка С’ будет иметь ту же абсциссу, что и С, то есть \(x_{C’} = x_C = 4\).
Ордината точки С’ будет находиться на таком же расстоянии от прямой \(у = 1\), как и ордината точки С, но с другой стороны.
Расстояние от С до прямой \(у = 1\) равно \(|-2 — 1| = |-3| = 3\).
Следовательно, ордината точки С’ будет \(y_{C’} = 1 + 3 = 4\).
Таким образом, точка, симметричная С(4; -2) относительно прямой \(у = 1\), имеет координаты С'(4; 4).
Ответы:
а) А(-1; 3),
б) С(4; 4)