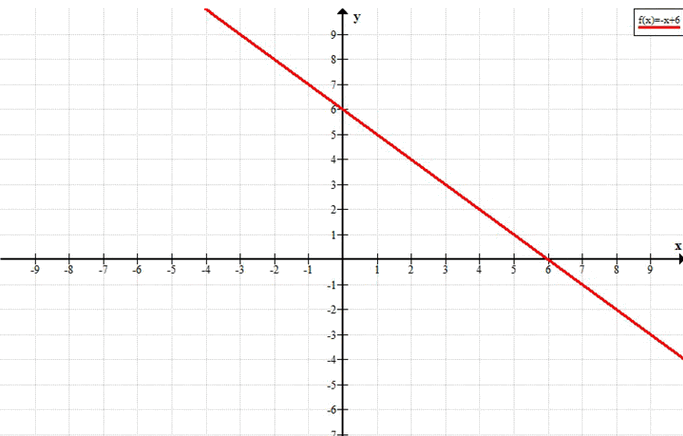ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 22 Мордкович — Подробные Ответы

Используя графический метод, решите неравенство: а) 4x + 8 < 0; б) -3х — 7 ≤ 2; в) 2х — 10 ≥ 0; г) -х + 6 > 4.

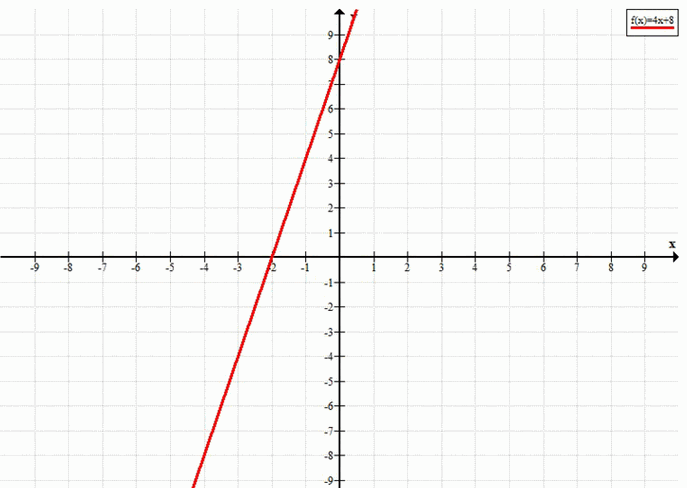
а) 4x + 8 < 0
y = 4x + 8, y < 0

Ответ: x < -2.

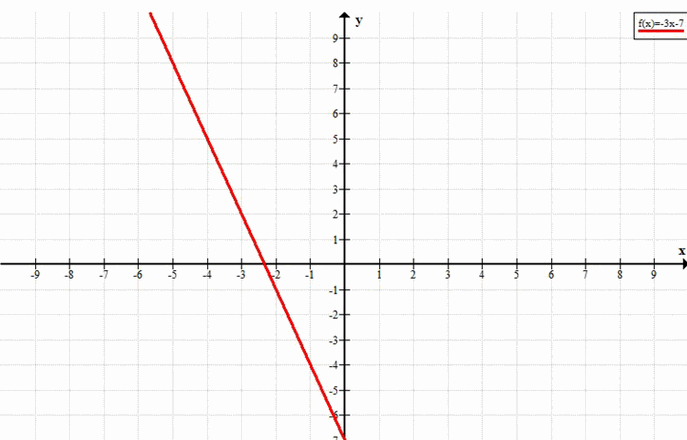
б) -3x — 7 ≤ 2
y = -3x — 7, y ≤ 2

Ответ: x ≥ -3.

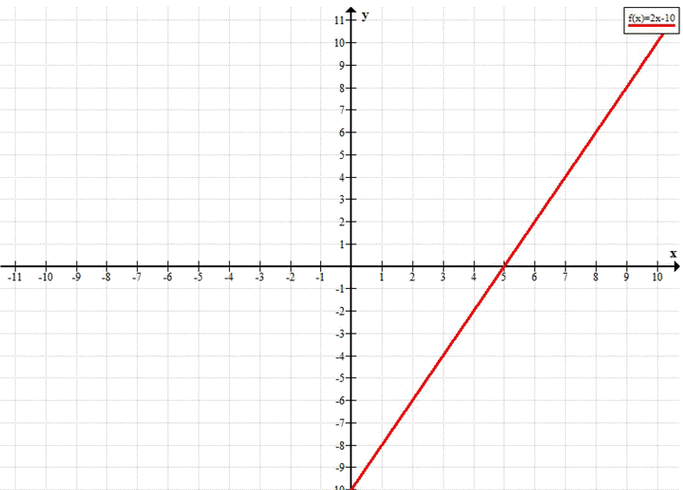
в) 2x — 10 ≥ 0
y = 2x — 10, y ≥ 0

Ответ: x ≥ 5.

г) -x + 6 > 4
y = -x + 6, y > 4

Ответ: x < 2.

а) Решим неравенство \(4x + 8 < 0\)

Рассмотрим линейную функцию \(y = 4x + 8\).
Неравенство \(4x + 8 < 0\) эквивалентно условию \(y < 0\), то есть нас интересуют те значения \(x\), при которых график функции находится ниже оси абсцисс.

Найдём точку пересечения графика с осью \(x\) (нуль функции):
\[
4x + 8 = 0 \quad \Rightarrow \quad 4x = -8 \quad \Rightarrow \quad x = -2.
\]

График — прямая с положительным угловым коэффициентом (наклон вверх направо), поэтому слева от точки \(x = -2\) функция отрицательна, а справа — положительна.

Следовательно, \(y < 0\) при всех \(x < -2\).

Ответ: \(x < -2\).

б) Решим неравенство \(-3x — 7 \leq 2\)

Перепишем его в виде:
\[
-3x — 7 \leq 2 \quad \Leftrightarrow \quad y \leq 2, \text{ где } y = -3x — 7.
\]

Но удобнее сначала решить алгебраически. Перенесём все члены в одну сторону:
\[
-3x \leq 2 + 7 \quad \Rightarrow \quad -3x \leq 9.
\]

Разделим обе части на \(-3\). Важно: при делении на отрицательное число знак неравенства меняется:
\[
x \geq -3.
\]

Графическая интерпретация: функция \(y = -3x — 7\) — убывающая прямая.
Условие \(y \leq 2\) означает, что мы ищем точки, лежащие на или ниже горизонтальной прямой \(y = 2\).
Это происходит при всех \(x\), начиная с \(-3\) и правее.

Ответ: \(x \geq -3\).

в) Решим неравенство \(2x — 10 \geq 0\)

Рассмотрим функцию \(y = 2x — 10\).
Неравенство \(2x — 10 \geq 0\) означает \(y \geq 0\) — график находится на или выше оси \(x\).

Найдём нуль функции:
\[
2x — 10 = 0 \quad \Rightarrow \quad 2x = 10 \quad \Rightarrow \quad x = 5.
\]

Поскольку угловой коэффициент положителен, функция возрастает: слева от \(x = 5\) — отрицательна, справа — положительна.

Следовательно, \(y \geq 0\) при \(x \geq 5\).

Ответ: \(x \geq 5\).

г) Решим неравенство \(-x + 6 > 4\)

Сначала упростим:
\[
-x + 6 > 4 \quad \Rightarrow \quad -x > -2.
\]

Умножим обе части на \(-1\), не забывая изменить знак неравенства:
\[
x < 2.
\]

Графическая интерпретация: функция \(y = -x + 6\) — убывающая прямая.
Условие \(y > 4\) означает, что график лежит выше горизонтальной прямой \(y = 4\).
Точка пересечения: \(-x + 6 = 4 \Rightarrow x = 2\).
Поскольку функция убывает, она выше уровня 4 слева от этой точки.

Ответ: \(x < 2\).