ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 23 Мордкович — Подробные Ответы

Постройте график уравнения: а) 2x + у — 4 = 0; б) -х — 2у + 6 = 0; в) -х — у + 1 = 0; г) 3x + 4у — 12 = 0.

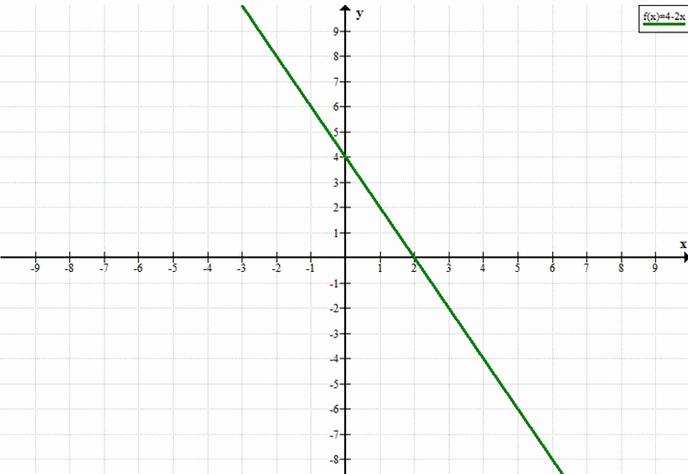
а) 2x + y — 4 = 0
y = 4 — 2x

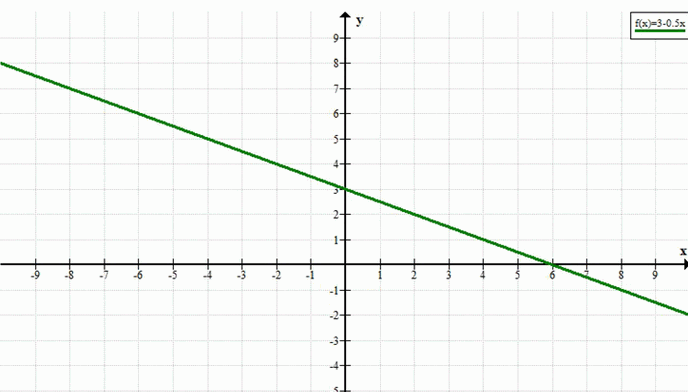
б) -x — 2y + 6 = 0
2y = 6 — x
y = 3 — 0,5x

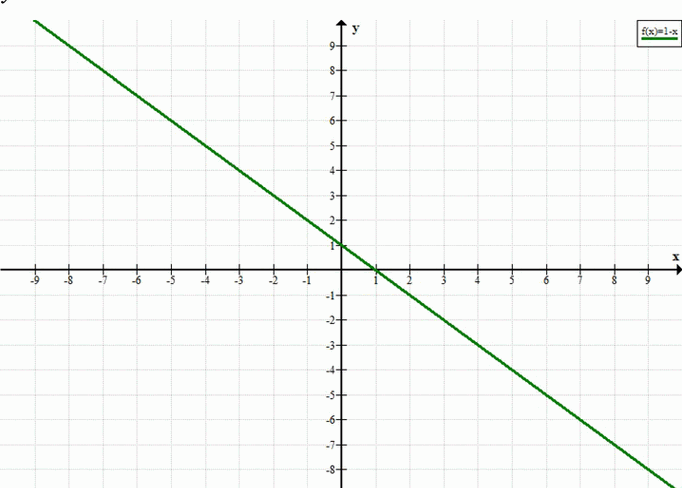
в) -x — y + 1 = 0
y = 1 — x

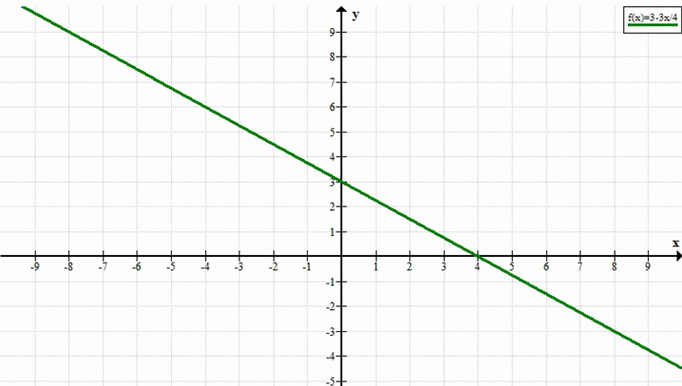
г) 3x + 4y — 12 = 0
4y = 12 — 3x
y = 3 — \(\frac{3}{4}x\)

а) Уравнение: \(2x + y — 4 = 0\)

Это линейное уравнение с двумя переменными. Чтобы построить его график, удобно выразить \(y\) через \(x\), то есть привести уравнение к виду \(y = kx + b\), где \(k\) — угловой коэффициент, а \(b\) — свободный член (ордината точки пересечения с осью \(y\)).

Перенесём все члены, кроме \(y\), в правую часть:
\[
y = -2x + 4,
\]

или, что то же самое,
\[
y = 4 — 2x.
\]

Графиком является прямая.
— При \(x = 0\): \(y = 4\) → точка \((0; 4)\).
— При \(y = 0\): \(0 = 4 — 2x \Rightarrow x = 2\) → точка \((2; 0)\).

Прямая проходит через эти две точки и имеет отрицательный наклон (убывает).

б) Уравнение: \(-x — 2y + 6 = 0\)

Снова выразим \(y\) через \(x\). Сначала перенесём члены с \(x\) и свободный член вправо:
\[
-2y = x — 6.
\]

Умножим обе части на \(-1\):
\[
2y = -x + 6 \quad \text{или} \quad 2y = 6 — x.
\]

Теперь разделим обе части на 2:
\[
y = \frac{6 — x}{2} = 3 — \frac{x}{2} = 3 — 0{,}5x.
\]

График — прямая с угловым коэффициентом \(-0{,}5\).
— При \(x = 0\): \(y = 3\) → точка \((0; 3)\).
— При \(y = 0\): \(0 = 3 — 0{,}5x \Rightarrow x = 6\) → точка \((6; 0)\).

Прямая убывает, но менее круто, чем в пункте а.

в) Уравнение: \(-x — y + 1 = 0\)

Выразим \(y\):
\[
-y = x — 1 \quad \Rightarrow \quad y = -x + 1 \quad \text{или} \quad y = 1 — x.
\]

Это уравнение прямой с угловым коэффициентом \(-1\), то есть она образует угол \(135^\circ\) с положительным направлением оси \(x\).
— При \(x = 0\): \(y = 1\) → точка \((0; 1)\).
— При \(y = 0\): \(0 = 1 — x \Rightarrow x = 1\) → точка \((1; 0)\).

Прямая проходит через эти точки и симметрична относительно биссектрисы второго и четвёртого координатных углов.

г) Уравнение: \(3x + 4y — 12 = 0\)

Выразим \(y\). Переносим остальные члены вправо:
\[
4y = -3x + 12 \quad \text{или} \quad 4y = 12 — 3x.
\]

Делим обе части на 4:
\[
y = \frac{12}{4} — \frac{3x}{4} = 3 — \frac{3}{4}x.
\]

График — прямая с угловым коэффициентом \(-\frac{3}{4}\).
— При \(x = 0\): \(y = 3\) → точка \((0; 3)\).
— При \(y = 0\): \(0 = 3 — \frac{3}{4}x \Rightarrow \frac{3}{4}x = 3 \Rightarrow x = 4\) → точка \((4; 0)\).

Прямая убывает, её наклон меньше по модулю, чем у прямой из пункта а, но больше, чем у прямой из пункта б.