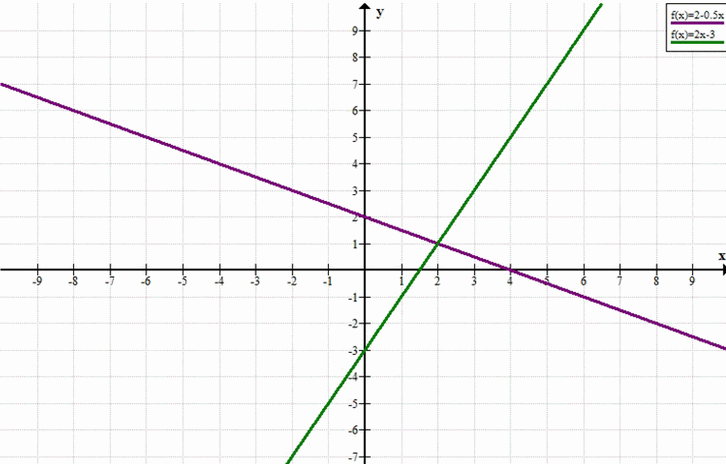Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 24 Мордкович — Подробные Ответы
Решите графически систему уравнений: а) система 3x+6y=0, 2x-y-5=0; б) система -x-2y+4=0, 2x-y-3=0; в) система 0,5x-2y=0, x-y-3=0; г) система x-3yy+6=0, -2x+y+3=0.
а)
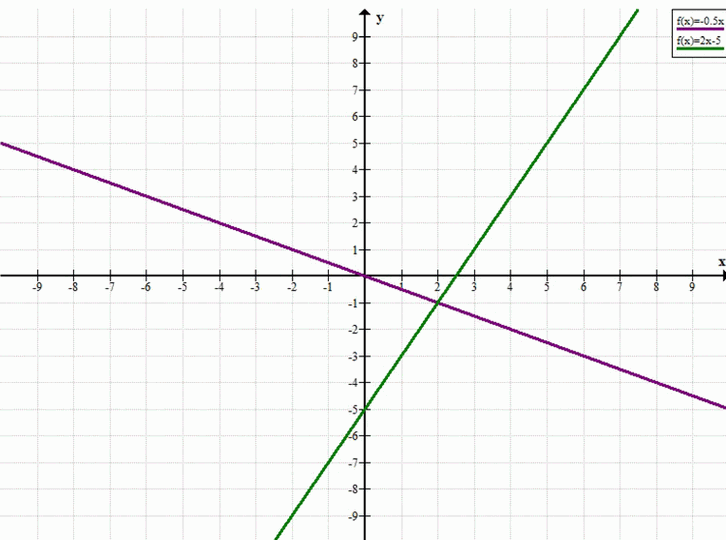
{ 3x + 6y = 0 → { 6y = -3x → { y = -0,5x
2x — y — 5 = 0 { y = 2x — 5 { y = 2x — 5
Ответ: (2; -1).
б)
{ -x — 2y + 4 = 0 → { 2y = 4 — x → { y = 2 — 0,5x
2x — y — 3 = 0 { y = 2x — 3 { y = 2x — 3
Ответ: (2; 1).
в)
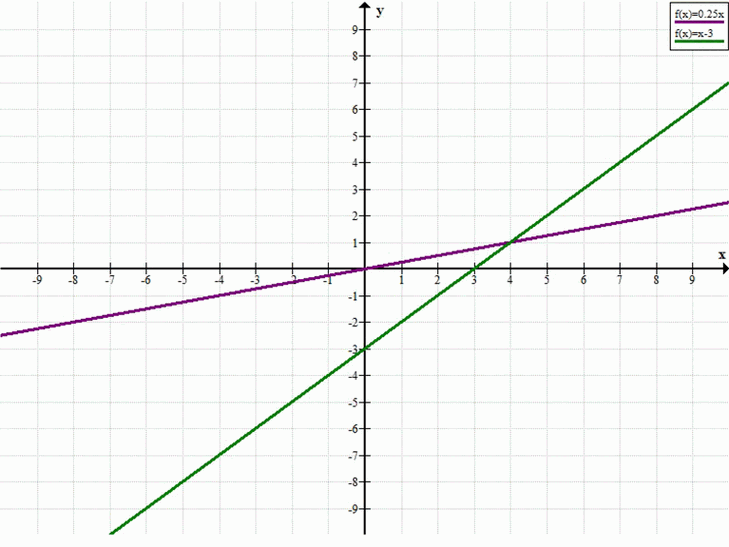
{ 0,5x — 2y = 0 → { 2y = 0,5x → { y = 0,25x
x — y — 3 = 0 { y = x — 3 { y = x — 3
Ответ: (4; 1).
г)
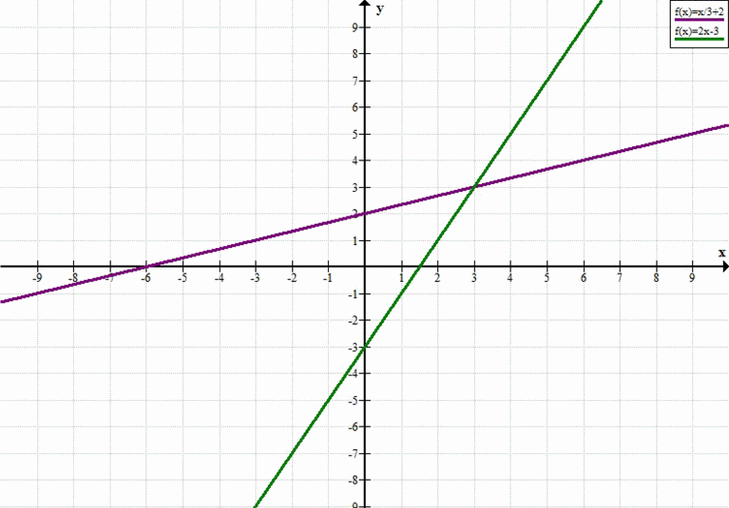
{ x — 3y + 6 = 0 → { 3y = x + 6 → { y = \frac{x}{3} + 2
-2x + y + 3 = 0 { y = 2x — 3 { y = 2x — 3
Ответ: (3; 3).
а) Система уравнений:
\[
\begin{cases}
3x + 6y = 0 \\
2x — y — 5 = 0
\end{cases}
\]
Приведём оба уравнения к виду \(y = kx + b\).
Из первого уравнения:
\(3x + 6y = 0 \Rightarrow 6y = -3x \Rightarrow y = -\frac{3}{6}x = -0{,}5x\).
Из второго уравнения:
\(2x — y — 5 = 0 \Rightarrow y = 2x — 5\).
Теперь приравняем правые части:
\(-0{,}5x = 2x — 5\).
Перенесём все члены с \(x\) в одну сторону:
\(-0{,}5x — 2x = -5 \Rightarrow -2{,}5x = -5\).
Разделим обе части на \(-2{,}5\):
\(x = \frac{-5}{-2{,}5} = 2\).
Подставим \(x = 2\) в любое из уравнений, например, во второе:
\(y = 2 \cdot 2 — 5 = 4 — 5 = -1\).
Проверка в первом уравнении:
\(3 \cdot 2 + 6 \cdot (-1) = 6 — 6 = 0\) — верно.
Ответ: \((2; -1)\).
б) Система уравнений:
\[
\begin{cases}
-x — 2y + 4 = 0 \\
2x — y — 3 = 0
\end{cases}
\]
Преобразуем:
Из первого уравнения:
\(-x — 2y + 4 = 0 \Rightarrow 2y = 4 — x \Rightarrow y = 2 — 0{,}5x\).
Из второго:
\(2x — y — 3 = 0 \Rightarrow y = 2x — 3\).
Приравниваем:
\(2 — 0{,}5x = 2x — 3\).
Переносим:
\(2 + 3 = 2x + 0{,}5x \Rightarrow 5 = 2{,}5x \Rightarrow x = \frac{5}{2{,}5} = 2\).
Находим \(y\):
\(y = 2 \cdot 2 — 3 = 4 — 3 = 1\).
Проверка в первом уравнении:
\(-2 — 2 \cdot 1 + 4 = -2 — 2 + 4 = 0\) — верно.
Ответ: \((2; 1)\).
в) Система уравнений:
\[
\begin{cases}
0{,}5x — 2y = 0 \\
x — y — 3 = 0
\end{cases}
\]
Преобразуем:
Из первого:
\(0{,}5x = 2y \Rightarrow y = \frac{0{,}5}{2}x = 0{,}25x\).
Из второго:
\(x — y — 3 = 0 \Rightarrow y = x — 3\).
Приравниваем:
\(0{,}25x = x — 3\).
Переносим:
\(0{,}25x — x = -3 \Rightarrow -0{,}75x = -3 \Rightarrow x = \frac{-3}{-0{,}75} = 4\).
Находим \(y\):
\(y = 4 — 3 = 1\).
Проверка в первом уравнении:
\(0{,}5 \cdot 4 — 2 \cdot 1 = 2 — 2 = 0\) — верно.
Ответ: \((4; 1)\).
г) Система уравнений:
\[
\begin{cases}
x — 3y + 6 = 0 \\
-2x + y + 3 = 0
\end{cases}
\]
Преобразуем:
Из первого:
\(x + 6 = 3y \Rightarrow y = \frac{x}{3} + 2\).
Из второго:
\(y = 2x — 3\).
Приравниваем:
\(\frac{x}{3} + 2 = 2x — 3\).
Умножим обе части на 3, чтобы избавиться от дроби:
\(x + 6 = 6x — 9\).
Переносим:
\(6 + 9 = 6x — x \Rightarrow 15 = 5x \Rightarrow x = 3\).
Находим \(y\):
\(y = 2 \cdot 3 — 3 = 6 — 3 = 3\).
Проверка в первом уравнении:
\(3 — 3 \cdot 3 + 6 = 3 — 9 + 6 = 0\) — верно.
Ответ: \((3; 3)\).