ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 28 Мордкович — Подробные Ответы

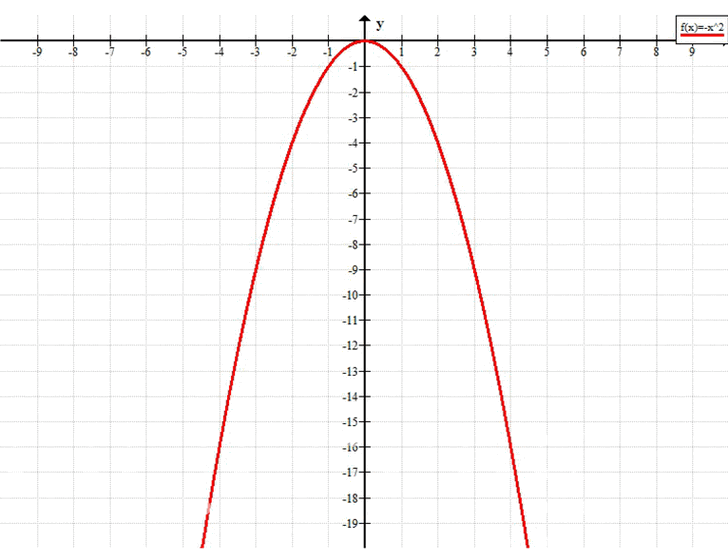
Постройте график функции у = -x². С помощью графика определите: а) значения функции, если значение аргумента равно -3; 1,5; 2; б) значения аргумента при значении функции, равном -1; 0; -9; в) наибольшее и наименьшее значения функции на отрезке [-1; 2]; г) значения х, при которых у < -9.

y = -x²

а) x = -3, y = -9;
x = 1,5, y = -2,25;
x = 2, y = -4.

б) y = -1, x = ±1;
y = 0, x = 0;
y = -9, x = ±3.

в) [-1; 2] — y_наим = -4, y_наиб = 0.

г) y ≤ -9 при x ∈ (-∞; -3] и [3; +∞).

Дано: функция \(y = -x^2\)

Это квадратичная функция, график которой — парабола, ветви направлены вниз, вершина находится в начале координат \((0; 0)\). Функция чётная: \(f(-x) = f(x)\), то есть симметрична относительно оси ординат. Область значений — все числа, не превышающие ноль: \(y \leq 0\).

а) Найдём значения функции при заданных значениях аргумента

Подставим указанные значения \(x\) в формулу \(y = -x^2\):

— При \(x = -3\):
\(y = -(-3)^2 = -9\).

— При \(x = 1{,}5\):
\(y = -(1{,}5)^2 = -2{,}25\).

— При \(x = 2\):
\(y = -(2)^2 = -4\).

Все значения отрицательны (кроме случая \(x = 0\), который здесь не рассматривается), что соответствует расположению графика целиком ниже или на уровне оси абсцисс.

б) Найдём значения аргумента, при которых функция принимает заданные значения

Решим уравнения вида \(-x^2 = y_0\), или эквивалентно \(x^2 = -y_0\).

— При \(y = -1\):
\(-x^2 = -1 \Rightarrow x^2 = 1 \Rightarrow x = \pm 1\).

— При \(y = 0\):
\(-x^2 = 0 \Rightarrow x = 0\).

— При \(y = -9\):
\(-x^2 = -9 \Rightarrow x^2 = 9 \Rightarrow x = \pm 3\).

Как и ожидалось для чётной функции, каждому положительному значению \(-y\) (то есть каждому отрицательному \(y\)) соответствуют два противоположных корня. Единственное решение при \(y = 0\) — это вершина параболы.

в) Найдём наименьшее и наибольшее значения функции на отрезке \([-1; 2]\)

На этом отрезке функция ведёт себя следующим образом:
— На промежутке \([-1; 0]\) она возрастает (так как слева от вершины парабола идёт вверх),
— На промежутке \([0; 2]\) — убывает (справа от вершины — вниз).

Следовательно, максимум достигается в вершине: при \(x = 0\), \(y = 0\).
Минимум — в той из концевых точек, где значение меньше:
— При \(x = -1\): \(y = -1\),
— При \(x = 2\): \(y = -4\).

Наименьшее значение — \(-4\), наибольшее — \(0\).

Таким образом, на отрезке \([-1; 2]\):
\(y_{\text{наим}} = -4\), \(y_{\text{наиб}} = 0\).

г) Решим неравенство \(y \leq -9\)

Подставим выражение функции:
\[
-x^2 \leq -9.
\]

Умножим обе части на \(-1\) (не забывая изменить знак неравенства):
\[
x^2 \geq 9.
\]

Это неравенство выполняется, когда \(|x| \geq 3\), то есть:
\[
x \leq -3 \quad \text{или} \quad x \geq 3.
\]

В интервальной записи:
\[
x \in (-\infty; -3] \cup [3; +\infty).
\]

Графически это означает, что часть параболы, лежащая на уровне или ниже горизонтальной прямой \(y = -9\), соответствует двум «хвостам» параболы — слева от \(-3\) и справа от \(3\).