ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 3 Мордкович — Подробные Ответы

а) Даны точки А(-1; 4) и В(-1; 8). Найдите прямую, которая является осью симметрии для этих двух точек. Отметьте точку С(-2; 5) и найдите точку, симметричную ей относительно найденной прямой. Укажите ещё одну пару симметричных точек, б) Даны точки К( 1; 5) и L(-3; 5). Найдите прямую, которая является осью симметрии для этих двух точек. Отметьте точку F(3; 7) и найдите точку, симметричную ей относительно найденной прямой. Укажите ещё одну пару симметричных точек.

а)
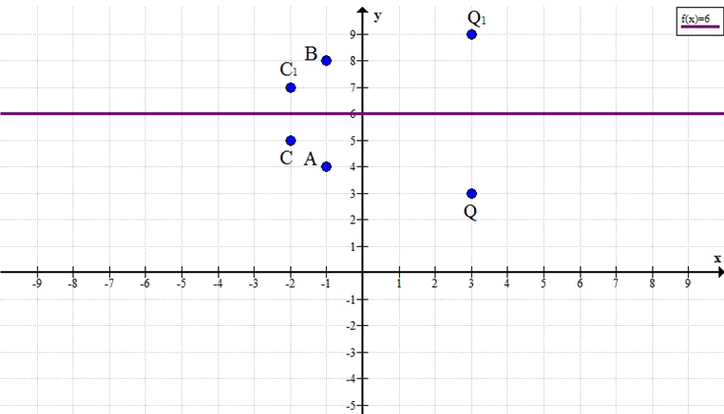
Точки А(-1; 4) и В(-1; 8) имеют одинаковую абсциссу.
Ось симметрии будет горизонтальной прямой, проходящей через середину отрезка АВ.
Координата y середины отрезка АВ: \( \frac{4 + 8}{2} = 6 \)
Уравнение оси симметрии: \( y = 6 \)
Точка С(-2; 5). Ищем точку C'(x’; y’), симметричную С относительно прямой \( y = 6 \).
Середина отрезка CC’ должна лежать на прямой \( y = 6 \).
\( \frac{5 + y’}{2} = 6 \)
\( 5 + y’ = 12 \)
\( y’ = 7 \)
Абсциссы точек C и C’ равны, так как симметрия происходит относительно горизонтальной прямой.
\( x’ = -2 \)
Симметричная точка C’ имеет координаты (-2; 7).
Еще одна пара симметричных точек: Возьмем точку D(-1; 6) на оси симметрии. Она симметрична сама себе. Возьмем точку E(-3; 6) на оси симметрии. Она симметрична сама себе.
Возьмем точку P(0; 6). Она симметрична сама себе.
Возьмем точку Q(0; 5). Ее симметричная точка Q’ будет иметь координаты (0; 7).

Ответ: \( y = 6 \), C'(-2; 7), Q(0; 5) и Q'(0; 7)

б)
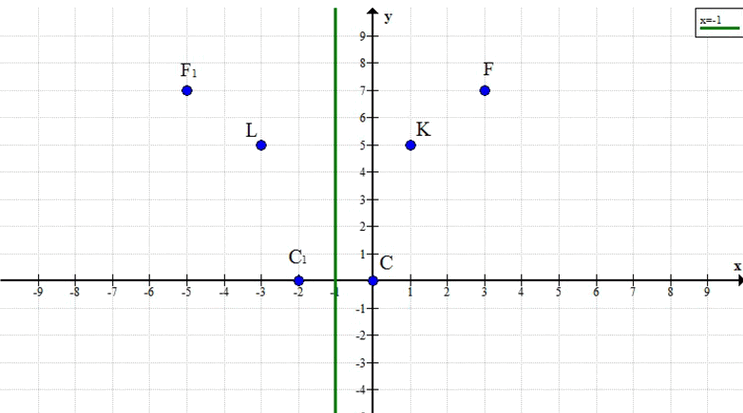
Точки К(1; 5) и L(-3; 5) имеют одинаковую ординату.
Ось симметрии будет вертикальной прямой, проходящей через середину отрезка KL.
Координата x середины отрезка KL: \( \frac{1 + (-3)}{2} = \frac{-2}{2} = -1 \)
Уравнение оси симметрии: \( x = -1 \)
Точка F(3; 7). Ищем точку F'(x’; y’), симметричную F относительно прямой \( x = -1 \).
Середина отрезка FF’ должна лежать на прямой \( x = -1 \).
\( \frac{3 + x’}{2} = -1 \)
\( 3 + x’ = -2 \)
\( x’ = -5 \)
Ординаты точек F и F’ равны, так как симметрия происходит относительно вертикальной прямой.
\( y’ = 7 \)
Симметричная точка F’ имеет координаты (-5; 7).
Еще одна пара симметричных точек: Возьмем точку M(-1; 0) на оси симметрии. Она симметрична сама себе. Возьмем точку N(-1; 10) на оси симметрии. Она симметрична сама себе.
Возьмем точку R(0; 0). Ее симметричная точка R’ будет иметь координаты (-2; 0).

Ответ: \( x = -1 \), F'(-5; 7), R(0; 0) и R'(-2; 0)

Условие: Найти оси симметрии для пар точек и симметричные точки относительно них.

Решение:

а)
Даны точки А(-1; 4) и В(-1; 8).
Ось симметрии для двух точек — это прямая, проходящая через середину отрезка, соединяющего эти точки, и перпендикулярная этому отрезку.
Координаты середины отрезка AB: \( M_{AB} = \left( \frac{-1 + (-1)}{2}, \frac{4 + 8}{2} \right) = \left( \frac{-2}{2}, \frac{12}{2} \right) = (-1, 6) \)
Отрезок AB имеет вид \( x = -1 \), что является вертикальной прямой.
Прямая, перпендикулярная вертикальной прямой, является горизонтальной прямой.
Таким образом, ось симметрии — это горизонтальная прямая, проходящая через середину отрезка AB.
Уравнение оси симметрии: \( y = 6 \)

Отмечена точка С(-2; 5).
Найдем точку C’, симметричную точке C(-2; 5) относительно прямой \( y = 6 \).
При симметрии относительно горизонтальной прямой \( y = k \), координата x точки остается прежней, а координата y изменяется так, чтобы середина отрезка, соединяющего исходную и симметричную точки, лежала на прямой \( y = k \).
Пусть C'(x’; y’).
\( x’ = -2 \)
\( \frac{5 + y’}{2} = 6 \)
\( 5 + y’ = 12 \)
\( y’ = 12 — 5 \)
\( y’ = 7 \)
Следовательно, точка C’ имеет координаты (-2; 7).

Укажем еще одну пару симметричных точек.
Возьмем точку D(0; 3).
Найдем точку D’, симметричную точке D(0; 3) относительно прямой \( y = 6 \).
\( x» = 0 \)
\( \frac{3 + y»}{2} = 6 \)
\( 3 + y» = 12 \)
\( y» = 12 — 3 \)
\( y» = 9 \)
Следовательно, точка D’ имеет координаты (0; 9).
Пара симметричных точек: D(0; 3) и D'(0; 9).

б)
Даны точки К(1; 5) и L(-3; 5).
Координаты середины отрезка KL: \( M_{KL} = \left( \frac{1 + (-3)}{2}, \frac{5 + 5}{2} \right) = \left( \frac{-2}{2}, \frac{10}{2} \right) = (-1, 5) \)
Отрезок KL имеет вид \( y = 5 \), что является горизонтальной прямой.
Прямая, перпендикулярная горизонтальной прямой, является вертикальной прямой.
Таким образом, ось симметрии — это вертикальная прямая, проходящая через середину отрезка KL.
Уравнение оси симметрии: \( x = -1 \)

Отмечена точка F(3; 7).
Найдем точку F’, симметричную точке F(3; 7) относительно прямой \( x = -1 \).
При симметрии относительно вертикальной прямой \( x = k \), координата y точки остается прежней, а координата x изменяется так, чтобы середина отрезка, соединяющего исходную и симметричную точки, лежала на прямой \( x = k \).
Пусть F'(x»; y»).
\( y» = 7 \)
\( \frac{3 + x»}{2} = -1 \)
\( 3 + x» = -2 \)
\( x» = -2 — 3 \)
\( x» = -5 \)
Следовательно, точка F’ имеет координаты (-5; 7).

Укажем еще одну пару симметричных точек.
Возьмем точку G(2; 1).
Найдем точку G’, симметричную точке G(2; 1) относительно прямой \( x = -1 \).
\( y»’ = 1 \)
\( \frac{2 + x»’}{2} = -1 \)
\( 2 + x»’ = -2 \)
\( x»’ = -2 — 2 \)
\( x»’ = -4 \)
Следовательно, точка G’ имеет координаты (-4; 1).
Пара симметричных точек: G(2; 1) и G'(-4; 1).

Ответы:
а) Ось симметрии: \( y = 6 \). Точка, симметричная С(-2; 5): C'(-2; 7). Еще одна пара симметричных точек: D(0; 3) и D'(0; 9).
б) Ось симметрии: \( x = -1 \). Точка, симметричная F(3; 7): F'(-5; 7). Еще одна пара симметричных точек: G(2; 1) и G'(-4; 1).