ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 30 Мордкович — Подробные Ответы

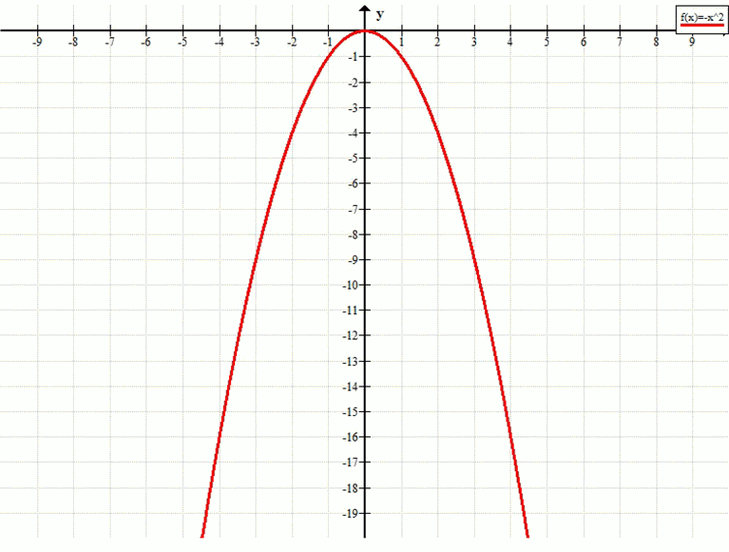
Постройте график функции у = -x². С помощью графика определите: а) значения функции, если х < -2; б) значения аргумента, если -9 ≤ у < -4; в) наибольшее значение функции; г) промежутки возрастания и убывания функции.

y = -x²

а) x < -2 при y < -4.
б) -9 ≤ y < -4 при x ∈ [-3; -2) и (2; 3].
в) y_наиб = 0.
г) функция возрастает при x ∈ (-∞; 0] и убывает при x ∈ [0; +∞).

Дано: функция \(y = -x^2\)

Это квадратичная функция, график которой — парабола, ветви направлены вниз, вершина находится в начале координат \((0; 0)\). Функция чётная (\(f(-x) = f(x)\)), непрерывна на всей числовой прямой. Область определения — \((-\infty; +\infty)\), область значений — \((-\infty; 0]\). Наибольшее значение функции равно 0 и достигается при \(x = 0\); наименьшего значения нет.

а) Условие: \(x < -2\) при \(y < -4\)

Рассмотрим неравенство \(y < -4\), то есть \(-x^2 < -4\).
Умножим обе части на \(-1\) (не забывая изменить знак неравенства):
\[
x^2 > 4.
\]

Это означает \(|x| > 2\), то есть \(x < -2\) или \(x > 2\).

Однако в условии указано только \(x < -2\). Это соответствует левой части графика, где функция возрастает. Таким образом, утверждение следует понимать как:
> Если рассматривать только левую половину параболы (\(x \leq 0\)), то условие \(y < -4\) выполняется тогда и только тогда, когда \(x < -2\).

Это связано с тем, что на промежутке \((-\infty; 0]\) функция возрастает, поэтому меньшим значениям \(x\) соответствуют меньшие (более отрицательные) значения \(y\).

б) Условие: \(-9 \leq y < -4\) при \(x \in [-3; -2) \cup (2; 3]\)

Рассмотрим двойное неравенство:
\[
-9 \leq -x^2 < -4.
\]

Умножим все части на \(-1\) (меняя знаки неравенств):
\[
9 \geq x^2 > 4,
\]

или эквивалентно:
\[
4 < x^2 \leq 9.
\]

Решим:
— \(x^2 > 4 \Rightarrow |x| > 2 \Rightarrow x < -2\) или \(x > 2\),
— \(x^2 \leq 9 \Rightarrow |x| \leq 3 \Rightarrow -3 \leq x \leq 3\).

Пересечение даёт:
\[
x \in [-3; -2) \cup (2; 3].
\]

Пояснение:
— При \(x = -3\) и \(x = 3\): \(y = -9\) — включено, так как неравенство нестрогое снизу (\(y \geq -9\)),
— При \(x = -2\) и \(x = 2\): \(y = -4\), но неравенство строгое сверху (\(y < -4\)), поэтому эти точки не входят.

Таким образом, запись в условии полностью корректна и отражает симметричное расположение двух участков графика, где функция принимает значения от \(-9\) (включительно) до \(-4\) (не включительно).

в) Наибольшее значение функции: \(y_{\text{наиб}} = 0\)

Поскольку \(x^2 \geq 0\) для любого \(x\), то \(-x^2 \leq 0\).
Равенство достигается при \(x = 0\): \(y = -0^2 = 0\).

Следовательно, функция ограничена сверху числом 0, и это значение действительно является глобальным максимумом.
Наименьшего значения нет, так как при \(|x| \to \infty\) значение \(y\) стремится к \(-\infty\).

г) Монотонность функции

Функция \(y = -x^2\):
— возрастает на промежутке \((-\infty; 0]\): при движении слева направо к вершине значения \(y\) увеличиваются (становятся менее отрицательными),
— убывает на промежутке \([0; +\infty)\): после вершины значения \(y\) уменьшаются (становятся более отрицательными).

Точка \(x = 0\) является точкой максимума и разделяет два участка монотонности.

Это поведение подтверждается производной: \(y’ = -2x\), которая положительна при \(x < 0\), отрицательна при \(x > 0\), и равна нулю при \(x = 0\).