ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 33 Мордкович — Подробные Ответы

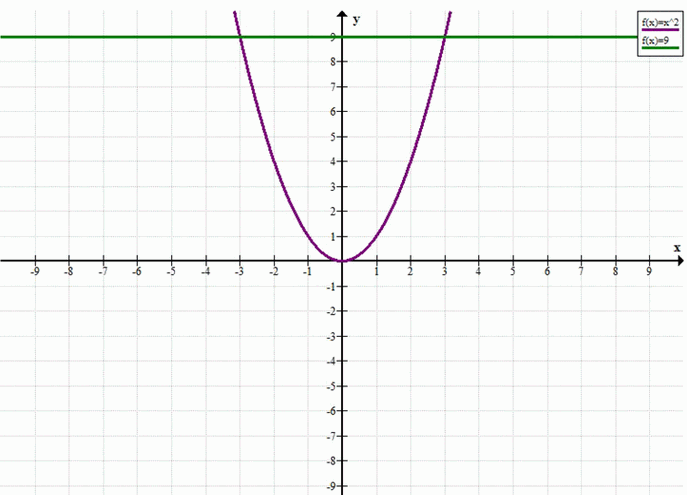
Решите графически уравнение: а) х2 = 9; б) -х2 = 2х; в) х2 = -3х; г) -х2 = 2.

а)
\( x^2 = 9 \)
\( x = \pm \sqrt{9} \)
\( x = \pm 3 \)

Ответ: -3; 3

б)
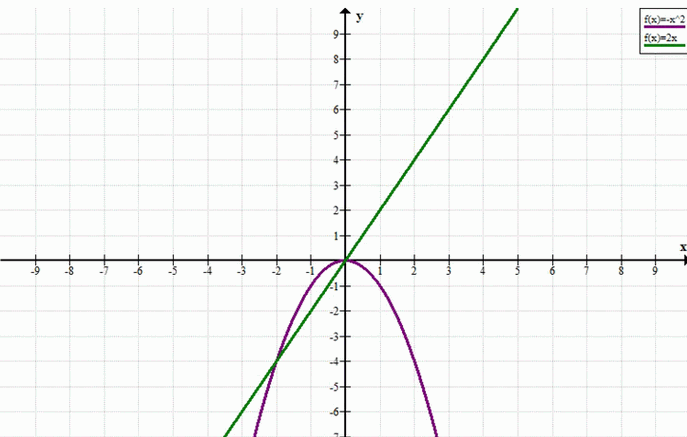
\( -x^2 = 2x \)
\( x^2 + 2x = 0 \)
\( x(x + 2) = 0 \)
\( x = 0 \)
\( x + 2 = 0 \)
\( x = -2 \)

Ответ: -2; 0

в)
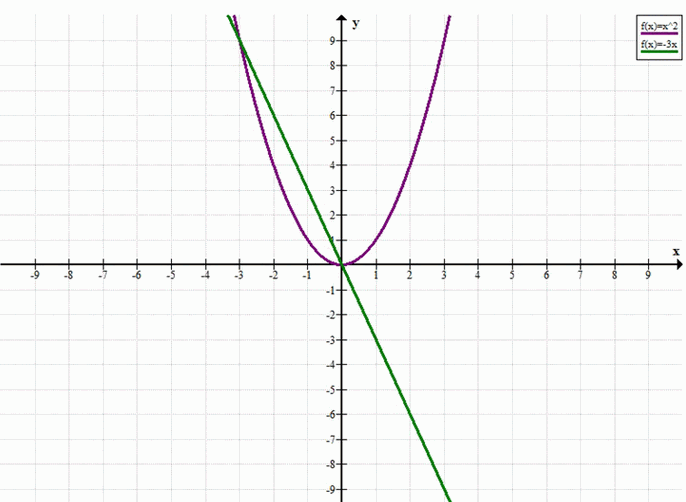
\( x^2 = -3x \)
\( x^2 + 3x = 0 \)
\( x(x + 3) = 0 \)
\( x = 0 \)
\( x + 3 = 0 \)
\( x = -3 \)

Ответ: -3; 0

г)
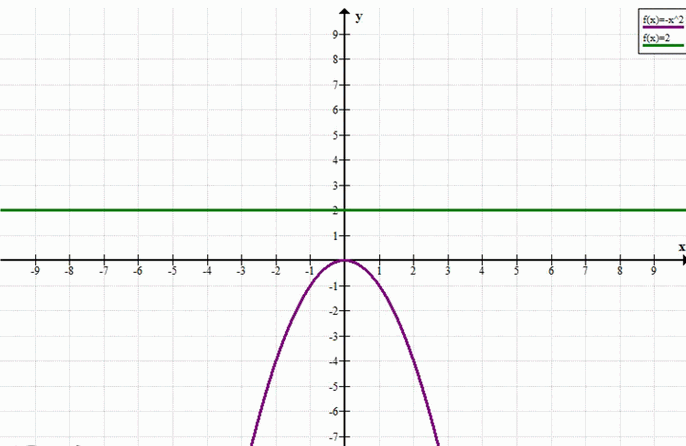
\( -x^2 = 2 \)
\( x^2 = -2 \)
\( x \in \emptyset \)

Ответ: \( \emptyset \)

а) Уравнение: \(x^2 = 9\)

Это простейшее квадратное уравнение. Чтобы найти все значения \(x\), при которых квадрат числа равен 9, извлекаем квадратный корень из обеих частей.
Поскольку квадратный корень из положительного числа имеет два значения — положительное и отрицательное, получаем:

\[
x = \pm \sqrt{9} = \pm 3.
\]

То есть уравнение имеет два действительных корня: \(x = -3\) и \(x = 3\).
Графически это означает, что парабола \(y = x^2\) пересекает горизонтальную прямую \(y = 9\) в двух точках, симметричных относительно оси ординат.

Ответ: \(-3; 3\).

б) Уравнение: \(-x^2 = 2x\)

Перенесём все члены в одну сторону, чтобы привести уравнение к стандартному виду:

\[
-x^2 — 2x = 0.
\]

Умножим обе части на \(-1\) (это не меняет множество решений):

\[
x^2 + 2x = 0.
\]

Теперь вынесем общий множитель \(x\) за скобки:

\[
x(x + 2) = 0.
\]

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно:

— либо \(x = 0\),
— либо \(x + 2 = 0 \Rightarrow x = -2\).

Оба значения удовлетворяют исходному уравнению:
— При \(x = 0\): \(-0^2 = 0\), \(2 \cdot 0 = 0\) — верно.
— При \(x = -2\): \(-(-2)^2 = -4\), \(2 \cdot (-2) = -4\) — верно.

Таким образом, уравнение имеет два корня.

Ответ: \(-2; 0\).

в) Уравнение: \(x^2 = -3x\)

Перенесём все слагаемые в левую часть:

\[
x^2 + 3x = 0.
\]

Вынесем общий множитель \(x\):

\[
x(x + 3) = 0.
\]

Решаем каждый множитель отдельно:
— \(x = 0\),
— \(x + 3 = 0 \Rightarrow x = -3\).

Проверка:
— При \(x = 0\): \(0^2 = 0\), \(-3 \cdot 0 = 0\) — верно.
— При \(x = -3\): \((-3)^2 = 9\), \(-3 \cdot (-3) = 9\) — верно.

Следовательно, оба корня допустимы.

Ответ: \(-3; 0\).

г) Уравнение: \(-x^2 = 2\)

Перепишем его, умножив обе части на \(-1\):

\[
x^2 = -2.
\]

Теперь проанализируем: квадрат любого действительного числа всегда неотрицателен, то есть \(x^2 \geq 0\) для всех \(x \in \mathbb{R}\).
Однако правая часть уравнения — отрицательное число (\(-2\)). Это означает, что не существует такого действительного числа, квадрат которого равен \(-2\).

Следовательно, уравнение не имеет решений в множестве действительных чисел. Множество решений пусто.

Ответ: \(\emptyset\).