Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 34 Мордкович — Подробные Ответы
а) -x² = х — 6; б) x² = 2х — 1; в) x² = 3х + 4; г) -x² = 4х + 4.
а)
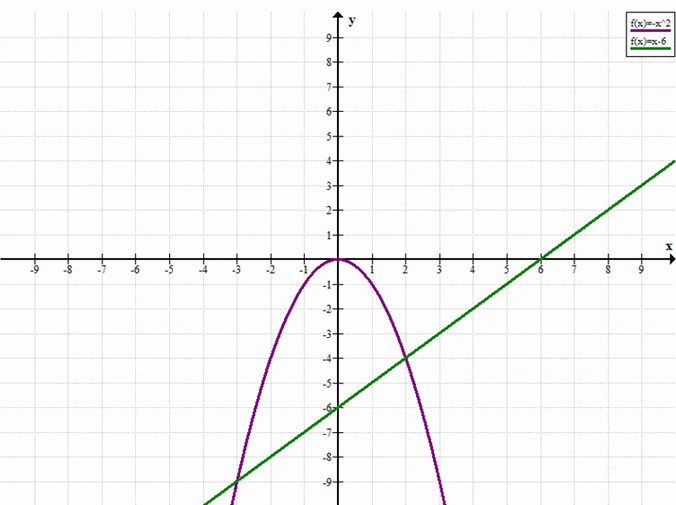
\( -x^2 = x — 6 \)
\( -x^2 — x + 6 = 0 \)
\( x^2 + x — 6 = 0 \)
\( D = 1^2 — 4 \cdot 1 \cdot (-6) \)
\( D = 1 + 24 \)
\( D = 25 \)
\( x = \frac{-1 \pm \sqrt{25}}{2 \cdot 1} \)
\( x = \frac{-1 \pm 5}{2} \)
\( x_1 = \frac{-1 + 5}{2} \)
\( x_1 = \frac{4}{2} \)
\( x_1 = 2 \)
\( x_2 = \frac{-1 — 5}{2} \)
\( x_2 = \frac{-6}{2} \)
\( x_2 = -3 \)
Ответ: -3; 2
б)
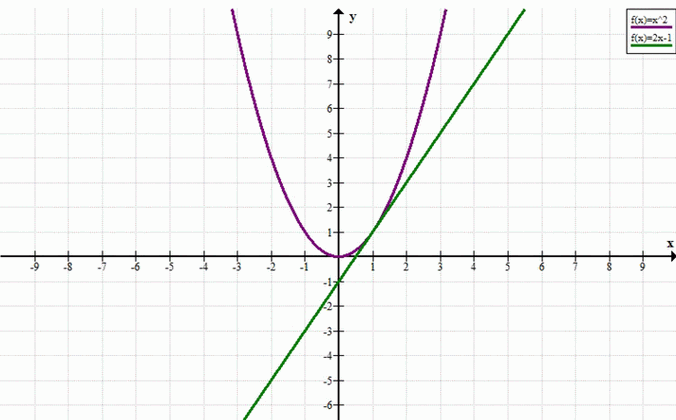
\( x^2 = 2x — 1 \)
\( x^2 — 2x + 1 = 0 \)
\( (x — 1)^2 = 0 \)
\( x — 1 = 0 \)
\( x = 1 \)
Ответ: 1
в)
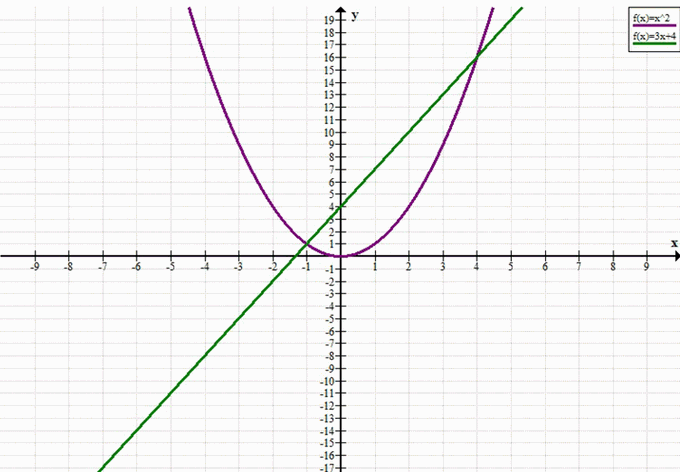
\( x^2 = 3x + 4 \)
\( x^2 — 3x — 4 = 0 \)
\( D = (-3)^2 — 4 \cdot 1 \cdot (-4) \)
\( D = 9 + 16 \)
\( D = 25 \)
\( x = \frac{-(-3) \pm \sqrt{25}}{2 \cdot 1} \)
\( x = \frac{3 \pm 5}{2} \)
\( x_1 = \frac{3 + 5}{2} \)
\( x_1 = \frac{8}{2} \)
\( x_1 = 4 \)
\( x_2 = \frac{3 — 5}{2} \)
\( x_2 = \frac{-2}{2} \)
\( x_2 = -1 \)
Ответ: -1; 4
г)
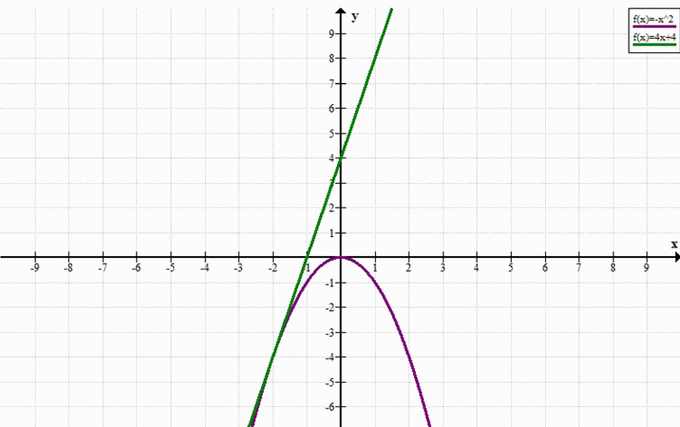
\( -x^2 = 4x + 4 \)
\( -x^2 — 4x — 4 = 0 \)
\( x^2 + 4x + 4 = 0 \)
\( (x + 2)^2 = 0 \)
\( x + 2 = 0 \)
\( x = -2 \)
Ответ: -2
Условие: Решить уравнение \( -x^2 = x — 6 \)
Решение:
Перенесем все члены уравнения в одну сторону, чтобы получить стандартный вид квадратного уравнения \( ax^2 + bx + c = 0 \):
\( -x^2 = x — 6 \)
\( 0 = x^2 + x — 6 \)
Или, что то же самое:
\( x^2 + x — 6 = 0 \)
Найдем дискриминант \( D \) по формуле \( D = b^2 — 4ac \):
Здесь \( a = 1 \), \( b = 1 \), \( c = -6 \).
\( D = 1^2 — 4 \cdot 1 \cdot (-6) \)
\( D = 1 + 24 \)
\( D = 25 \)
Так как \( D > 0 \), уравнение имеет два различных действительных корня.
Найдем корни по формуле \( x = \frac{-b \pm \sqrt{D}}{2a} \):
\( x_1 = \frac{-1 + \sqrt{25}}{2 \cdot 1} \)
\( x_1 = \frac{-1 + 5}{2} \)
\( x_1 = \frac{4}{2} \)
\( x_1 = 2 \)
\( x_2 = \frac{-1 — \sqrt{25}}{2 \cdot 1} \)
\( x_2 = \frac{-1 — 5}{2} \)
\( x_2 = \frac{-6}{2} \)
\( x_2 = -3 \)
Ответ: -3; 2
Условие: Решить уравнение \( x^2 = 2x — 1 \)
Решение:
Перенесем все члены уравнения в одну сторону:
\( x^2 = 2x — 1 \)
\( x^2 — 2x + 1 = 0 \)
Заметим, что левая часть уравнения является полным квадратом:
\( (x — 1)^2 = 0 \)
Извлечем квадратный корень из обеих частей:
\( x — 1 = 0 \)
\( x = 1 \)
Ответ: 1
Условие: Решить уравнение \( x^2 = 3x + 4 \)
Решение:
Перенесем все члены уравнения в одну сторону, чтобы получить стандартный вид квадратного уравнения \( ax^2 + bx + c = 0 \):
\( x^2 = 3x + 4 \)
\( x^2 — 3x — 4 = 0 \)
Найдем дискриминант \( D \) по формуле \( D = b^2 — 4ac \):
Здесь \( a = 1 \), \( b = -3 \), \( c = -4 \).
\( D = (-3)^2 — 4 \cdot 1 \cdot (-4) \)
\( D = 9 + 16 \)
\( D = 25 \)
Так как \( D > 0 \), уравнение имеет два различных действительных корня.
Найдем корни по формуле \( x = \frac{-b \pm \sqrt{D}}{2a} \):
\( x_1 = \frac{-(-3) + \sqrt{25}}{2 \cdot 1} \)
\( x_1 = \frac{3 + 5}{2} \)
\( x_1 = \frac{8}{2} \)
\( x_1 = 4 \)
\( x_2 = \frac{-(-3) — \sqrt{25}}{2 \cdot 1} \)
\( x_2 = \frac{3 — 5}{2} \)
\( x_2 = \frac{-2}{2} \)
\( x_2 = -1 \)
Ответ: -1; 4
Условие: Решить уравнение \( -x^2 = 4x + 4 \)
Решение:
Перенесем все члены уравнения в одну сторону, чтобы получить стандартный вид квадратного уравнения \( ax^2 + bx + c = 0 \):
\( -x^2 = 4x + 4 \)
\( 0 = x^2 + 4x + 4 \)
Или, что то же самое:
\( x^2 + 4x + 4 = 0 \)
Заметим, что левая часть уравнения является полным квадратом:
\( (x + 2)^2 = 0 \)
Извлечем квадратный корень из обеих частей:
\( x + 2 = 0 \)
\( x = -2 \)
Ответ: -2