ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 35 Мордкович — Подробные Ответы

Решите графически неравенство: а) x² > 4; б) -x² > х — 2; в) -x² > -9; г) x² < 2 + х.

а)
\( x^2 > 4 \)
\( y_1 = x^2 \)
\( y_2 = 4 \)
\( x^2 = 4 \)
\( x = -2 \)
\( x = 2 \)
\( x \in (-\infty; -2) \cup (2; +\infty) \)

Ответ: \( (-\infty; -2) \cup (2; +\infty) \)

б)
\( -x^2 > x — 2 \)
\( y_1 = -x^2 \)
\( y_2 = x — 2 \)
\( -x^2 = x — 2 \)
\( x^2 + x — 2 = 0 \)
\( (x + 2)(x — 1) = 0 \)
\( x = -2 \)
\( x = 1 \)
\( x \in (-2; 1) \)

Ответ: \( (-2; 1) \)

в)
\( -x^2 > -9 \)
\( y_1 = -x^2 \)
\( y_2 = -9 \)
\( -x^2 = -9 \)
\( x^2 = 9 \)
\( x = -3 \)
\( x = 3 \)
\( x \in (-3; 3) \)

Ответ: \( (-3; 3) \)

г)
\( x^2 < 2 + x \)
\( y_1 = x^2 \)
\( y_2 = 2 + x \)
\( x^2 = 2 + x \)
\( x^2 — x — 2 = 0 \)
\( (x — 2)(x + 1) = 0 \)
\( x = -1 \)
\( x = 2 \)
\( x \in (-1; 2) \)

Ответ: \( (-1; 2) \)

Условие: Решите графически неравенство:

а)
\( x^2 > 4 \);

б)
\( -x^2 > x — 2 \);

в)
\( -x^2 > -9 \);

г)
\( x^2 < 2 + x \).

Решение:

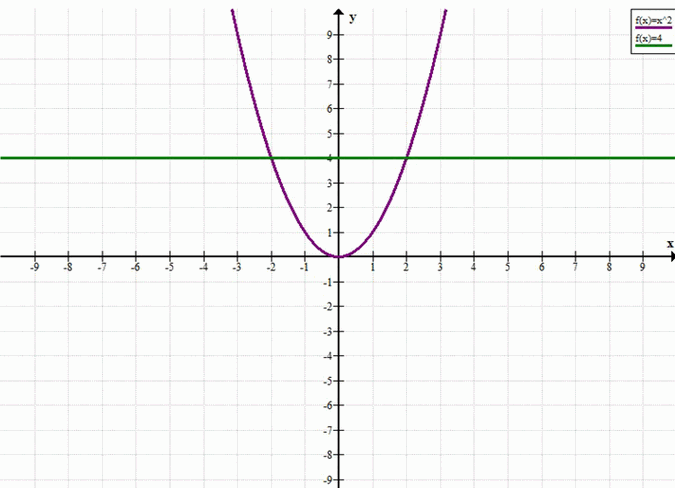
а) Решим неравенство \( x^2 > 4 \).
Построим графики функций \( y = x^2 \) и \( y = 4 \).
Графиком функции \( y = x^2 \) является парабола, ветви которой направлены вверх, вершина находится в начале координат.
Графиком функции \( y = 4 \) является прямая, параллельная оси абсцисс и проходящая через точку \( (0; 4) \).
Найдем точки пересечения графиков, приравняв правые части уравнений:
\( x^2 = 4 \)
\( x = \pm \sqrt{4} \)
\( x_1 = -2 \)
\( x_2 = 2 \)
Неравенство \( x^2 > 4 \) выполняется, когда график функции \( y = x^2 \) расположен выше графика функции \( y = 4 \).
Это происходит при \( x < -2 \) или \( x > 2 \).

Таким образом, решением неравенства является объединение интервалов \( (-\infty; -2) \cup (2; +\infty) \).

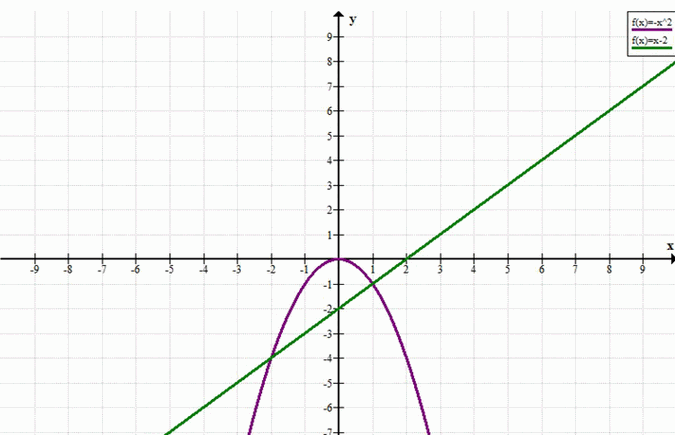
б) Решим неравенство \( -x^2 > x — 2 \).
Построим графики функций \( y = -x^2 \) и \( y = x — 2 \).
Графиком функции \( y = -x^2 \) является парабола, ветви которой направлены вниз, вершина находится в начале координат.
Графиком функции \( y = x — 2 \) является прямая.
Найдем точки пересечения графиков, приравняв правые части уравнений:
\( -x^2 = x — 2 \)
Перенесем все члены в одну сторону:
\( x^2 + x — 2 = 0 \)
Решим квадратное уравнение, используя формулу для корней квадратного уравнения \( x = \frac{-b \pm \sqrt{D}}{2a} \), где \( D = b^2 — 4ac \).
Найдем дискриминант: \( D = 1^2 — 4 \cdot 1 \cdot (-2) = 1 + 8 = 9 \)
\( x = \frac{-1 \pm \sqrt{9}}{2 \cdot 1} \)
\( x = \frac{-1 \pm 3}{2} \)
\( x_1 = \frac{-1 — 3}{2} = \frac{-4}{2} = -2 \)
\( x_2 = \frac{-1 + 3}{2} = \frac{2}{2} = 1 \)
Неравенство \( -x^2 > x — 2 \) выполняется, когда график функции \( y = -x^2 \) расположен выше графика функции \( y = x — 2 \).
Это происходит между точками пересечения, то есть при \( -2 < x < 1 \).

Таким образом, решением неравенства является интервал \( (-2; 1) \).

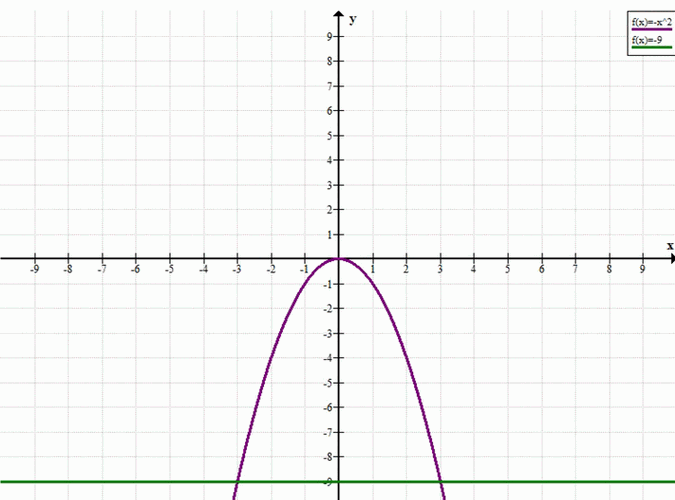
в) Решим неравенство \( -x^2 > -9 \).
Построим графики функций \( y = -x^2 \) и \( y = -9 \).
Графиком функции \( y = -x^2 \) является парабола, ветви которой направлены вниз, вершина находится в начале координат.
Графиком функции \( y = -9 \) является прямая, параллельная оси абсцисс и проходящая через точку \( (0; -9) \).
Найдем точки пересечения графиков, приравняв правые части уравнений:
\( -x^2 = -9 \)
Умножим обе части на \( -1 \):
\( x^2 = 9 \)
\( x = \pm \sqrt{9} \)
\( x_1 = -3 \)
\( x_2 = 3 \)
Неравенство \( -x^2 > -9 \) выполняется, когда график функции \( y = -x^2 \) расположен выше графика функции \( y = -9 \).
Это происходит между точками пересечения, то есть при \( -3 < x < 3 \).

Таким образом, решением неравенства является интервал \( (-3; 3) \).

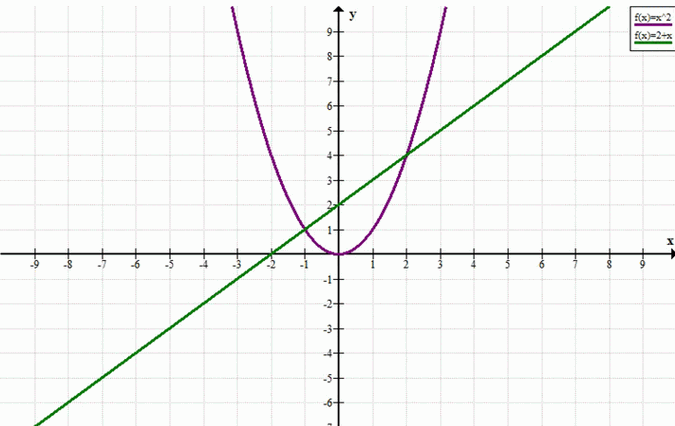
г) Решим неравенство \( x^2 < 2 + x \).
Построим графики функций \( y = x^2 \) и \( y = 2 + x \).
Графиком функции \( y = x^2 \) является парабола, ветви которой направлены вверх, вершина находится в начале координат.
Графиком функции \( y = 2 + x \) является прямая.
Найдем точки пересечения графиков, приравняв правые части уравнений:
\( x^2 = 2 + x \)
Перенесем все члены в одну сторону:
\( x^2 — x — 2 = 0 \)
Решим квадратное уравнение, используя формулу для корней квадратного уравнения \( x = \frac{-b \pm \sqrt{D}}{2a} \), где \( D = b^2 — 4ac \).
Найдем дискриминант: \( D = (-1)^2 — 4 \cdot 1 \cdot (-2) = 1 + 8 = 9 \)
\( x = \frac{-(-1) \pm \sqrt{9}}{2 \cdot 1} \)
\( x = \frac{1 \pm 3}{2} \)
\( x_1 = \frac{1 — 3}{2} = \frac{-2}{2} = -1 \)
\( x_2 = \frac{1 + 3}{2} = \frac{4}{2} = 2 \)
Неравенство \( x^2 < 2 + x \) выполняется, когда график функции \( y = x^2 \) расположен ниже графика функции \( y = 2 + x \).
Это происходит между точками пересечения, то есть при \( -1 < x < 2 \).

Таким образом, решением неравенства является интервал \( (-1; 2) \).

Ответ:

а)
\( (-\infty; -2) \cup (2; +\infty) \);

б)
\( (-2; 1) \);

в)
\( (-3; 3) \);

г)
\( (-1; 2) \)