ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 37 Мордкович — Подробные Ответы

Постройте график функции у = f(x), где f(x) = система -x², если -2 ≤ х ≤ О, 2х, если 0 < х ≤ 2. С помощью графика найдите: а) f(-1), f(О), f(2); б) значения х, при которых f(x) = 0, f(х) = -4, f(x) = 1; в) область определения функции; г) множество значений функции.

Функция задана следующим образом:
\( f(x) = \begin{cases} -x^2, & \text{если } -2 \le x \le 0 \\ 2x, & \text{если } 0 < x \le 2 \end{cases} \)

а)
\( f(-1), f(0), f(2) \)
Для \( f(-1) \):
\( -2 \le -1 \le 0 \)
\( f(-1) = -(-1)^2 \)
\( f(-1) = -1 \)

Для \( f(0) \):
\( -2 \le 0 \le 0 \)
\( f(0) = -(0)^2 \)
\( f(0) = 0 \)

Для \( f(2) \):
\( 0 < 2 \le 2 \)
\( f(2) = 2 \cdot 2 \)
\( f(2) = 4 \)
Ответ: \( f(-1) = -1, f(0) = 0, f(2) = 4 \)

б) значения х, при которых \( f(x) = 0, f(x) = -4, f(x) = 1 \)

При \( f(x) = 0 \):
Рассмотрим первый интервал: \( -2 \le x \le 0 \)
\( -x^2 = 0 \)
\( x^2 = 0 \)
\( x = 0 \)
Значение \( x = 0 \) входит в интервал \( [-2, 0] \).

Рассмотрим второй интервал: \( 0 < x \le 2 \)
\( 2x = 0 \)
\( x = 0 \)
Значение \( x = 0 \) не входит в интервал \( (0, 2] \).
Ответ: \( x = 0 \)

При \( f(x) = -4 \):
Рассмотрим первый интервал: \( -2 \le x \le 0 \)
\( -x^2 = -4 \)
\( x^2 = 4 \)
\( x = \pm 2 \)
Значение \( x = -2 \) входит в интервал \( [-2, 0] \).
Значение \( x = 2 \) не входит в интервал \( [-2, 0] \).

Рассмотрим второй интервал: \( 0 < x \le 2 \)
\( 2x = -4 \)
\( x = -2 \)
Значение \( x = -2 \) не входит в интервал \( (0, 2] \).
Ответ: \( x = -2 \)

При \( f(x) = 1 \):
Рассмотрим первый интервал: \( -2 \le x \le 0 \)
\( -x^2 = 1 \)
\( x^2 = -1 \)
Действительных решений нет.

Рассмотрим второй интервал: \( 0 < x \le 2 \)
\( 2x = 1 \)
\( x = \frac{1}{2} \)
Значение \( x = \frac{1}{2} \) входит в интервал \( (0, 2] \).
Ответ: \( x = \frac{1}{2} \)

в) область определения функции
Область определения первой части функции: \( [-2, 0] \)
Область определения второй части функции: \( (0, 2] \)
Объединение этих интервалов дает область определения всей функции:
\( [-2, 0] \cup (0, 2] = [-2, 2] \)
Ответ: \( [-2, 2] \)

г) множество значений функции
Для первой части функции \( y = -x^2 \) на интервале \( [-2, 0] \):
При \( x = -2 \), \( y = -(-2)^2 = -4 \)
При \( x = 0 \), \( y = -(0)^2 = 0 \)
Так как функция \( y = -x^2 \) возрастает на интервале \( [-2, 0] \), множество значений этой части: \( [-4, 0] \)

Для второй части функции \( y = 2x \) на интервале \( (0, 2] \):
При \( x \to 0^+ \), \( y \to 2 \cdot 0 = 0 \) (значение не включается)
При \( x = 2 \), \( y = 2 \cdot 2 = 4 \) (значение включается)
Так как функция \( y = 2x \) возрастает на интервале \( (0, 2] \), множество значений этой части: \( (0, 4] \)

Объединение множеств значений обеих частей функции:
\( [-4, 0] \cup (0, 4] = [-4, 4] \)
Ответ: \( [-4, 4] \)

Условие: Постройте график функции \(у = f(x)\), где \( f(x) = \begin{cases} -x^2, & \text{если } -2 \le x \le 0 \\ 2x, & \text{если } 0 < x \le 2 \end{cases} \). С помощью графика найдите:

а)
\( f(-1), f(0), f(2) \);

б) значения \( x \), при которых \( f(x) = 0, f(x) = -4, f(x) = 1 \);

в) область определения функции;

г) множество значений функции.

Решение:
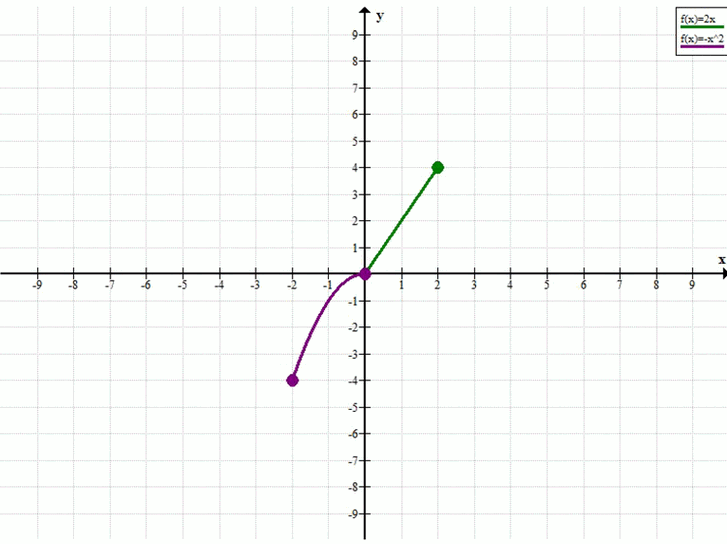
1. Построим график функции \( f(x) \). Функция является кусочно-заданной.
Для интервала \( -2 \le x \le 0 \), функция задана как \( y = -x^2 \). Это часть параболы, ветви которой направлены вниз, с вершиной в точке \( (0,0) \).
Вычислим значения в ключевых точках для этого интервала:
При \( x = -2 \), \( y = -(-2)^2 = -4 \). Точка \( (-2, -4) \).
При \( x = -1 \), \( y = -(-1)^2 = -1 \). Точка \( (-1, -1) \).
При \( x = 0 \), \( y = -(0)^2 = 0 \). Точка \( (0, 0) \).
Соединим эти точки плавной кривой.

Для интервала \( 0 < x \le 2 \), функция задана как \( y = 2x \). Это часть прямой линии.
Вычислим значения в ключевых точках для этого интервала:
При \( x \to 0^+ \), \( y \to 2(0) = 0 \). Точка \( (0, 0) \) является «выколотой» для этой части, но она уже включена первой частью функции.
При \( x = 1 \), \( y = 2(1) = 2 \). Точка \( (1, 2) \).
При \( x = 2 \), \( y = 2(2) = 4 \). Точка \( (2, 4) \).
Соединим эти точки прямой линией.

2. Найдем значения функции:

а)
\( f(-1), f(0), f(2) \)
Для \( f(-1) \): \( -1 \) находится в интервале \( -2 \le x \le 0 \), поэтому используем \( f(x) = -x^2 \).
\( f(-1) = -(-1)^2 = -1 \).
Для \( f(0) \): \( 0 \) находится в интервале \( -2 \le x \le 0 \), поэтому используем \( f(x) = -x^2 \).
\( f(0) = -(0)^2 = 0 \).
Для \( f(2) \): \( 2 \) находится в интервале \( 0 < x \le 2 \), поэтому используем \( f(x) = 2x \).
\( f(2) = 2(2) = 4 \).

3. Найдем значения \( x \), при которых \( f(x) \) принимает заданные значения:

б)
\( f(x) = 0, f(x) = -4, f(x) = 1 \)
Для \( f(x) = 0 \):
Рассмотрим первый интервал: \( -x^2 = 0 \Rightarrow x = 0 \). Это значение входит в интервал \( [-2, 0] \).
Рассмотрим второй интервал: \( 2x = 0 \Rightarrow x = 0 \). Это значение не входит в интервал \( (0, 2] \).
Следовательно, \( x = 0 \).
Для \( f(x) = -4 \):
Рассмотрим первый интервал: \( -x^2 = -4 \Rightarrow x^2 = 4 \Rightarrow x = \pm 2 \).
Значение \( x = -2 \) входит в интервал \( [-2, 0] \).
Значение \( x = 2 \) не входит в интервал \( [-2, 0] \).
Рассмотрим второй интервал: \( 2x = -4 \Rightarrow x = -2 \). Это значение не входит в интервал \( (0, 2] \).
Следовательно, \( x = -2 \).
Для \( f(x) = 1 \):
Рассмотрим первый интервал: \( -x^2 = 1 \Rightarrow x^2 = -1 \). Нет действительных решений.
Рассмотрим второй интервал: \( 2x = 1 \Rightarrow x = 1/2 \). Это значение входит в интервал \( (0, 2] \).
Следовательно, \( x = 1/2 \).

4. Найдем область определения функции:

в) Область определения функции \( D(f) \) — это все значения \( x \), для которых функция определена.
Функция определена для \( x \in [-2, 0] \) и для \( x \in (0, 2] \).
Объединяя эти интервалы, получаем \( D(f) = [-2, 2] \).

5. Найдем множество значений функции:
г) Множество значений функции \( E(f) \) — это все значения \( y \), которые принимает функция.
Для части \( y = -x^2 \) на интервале \( [-2, 0] \):
Минимальное значение \( y = -(-2)^2 = -4 \) при \( x = -2 \).
Максимальное значение \( y = -(0)^2 = 0 \) при \( x = 0 \).
Множество значений для этой части: \( [-4, 0] \).
Для части \( y = 2x \) на интервале \( (0, 2] \):
При \( x \to 0^+ \), \( y \to 0^+ \).
Максимальное значение \( y = 2(2) = 4 \) при \( x = 2 \).
Множество значений для этой части: \( (0, 4] \).
Объединяя множества значений \( [-4, 0] \) и \( (0, 4] \), получаем \( E(f) = [-4, 4] \).

Ответы:

а)
\( f(-1) = -1, f(0) = 0, f(2) = 4 \);

б) при \( f(x) = 0, x = 0 \); при \( f(x) = -4, x = -2 \); при \( f(x) = 1, x = 1/2 \);

в)
\( D(f) = [-2, 2] \);

г)
\( E(f) = [-4, 4] \).