ГДЗ по Алгебре 7 Класс Итоговое Повторение Номер 4 Мордкович — Подробные Ответы

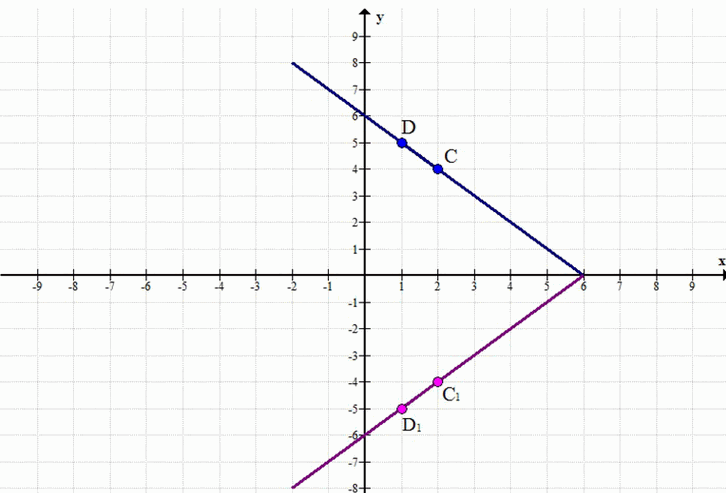
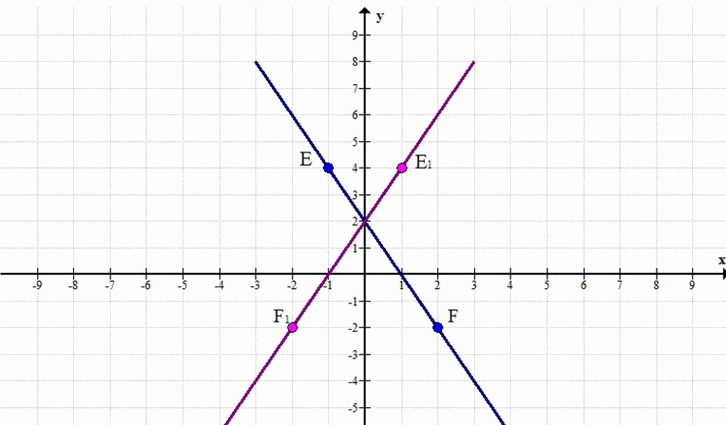
а) Даны точки С(2; 4) и D( 1; 5). Постройте прямую, симметричную прямой CD относительно оси абсцисс, б) Даны точки ?(-1; 4) и F(2; -2). Постройте прямую, симметричную прямой EF относительно оси ординат.

а)
Точки \(C(2,4)\) и \(D(1,5)\) при симметрии относительно оси абсцисс переходят в \(C'(2,-4)\) и \(D'(1,-5)\).
Уравнение прямой через них:
\[
\frac{y + 4}{-1} = \frac{x — 2}{-1} \;\Rightarrow\; y + 4 = x — 2 \;\Rightarrow\; y = x — 6.
\]

Ответ: \(y = x — 6\).

б)
Точки \(E(-1,4)\) и \(F(2,-2)\) при симметрии относительно оси ординат переходят в \(E»(1,4)\) и \(F»(-2,-2)\).
Уравнение прямой через них:
\[
\frac{y — 4}{-6} = \frac{x — 1}{-3} \;\Rightarrow\; y — 4 = 2(x — 1) \;\Rightarrow\; y = 2x + 2.
\]

Ответ: \(y = 2x + 2\).

а)
Пусть точка C имеет координаты \( (x_C, y_C) \) и точка D имеет координаты \( (x_D, y_D) \).
\( C = (2, 4) \)
\( D = (1, 5) \)
Прямая, симметричная прямой CD относительно оси абсцисс, будет проходить через точки C’ и D’, где координаты этих точек являются отражением C и D относительно оси абсцисс.
Для отражения относительно оси абсцисс, координата x остается прежней, а координата y меняет знак.
\( C’ = (x_C, -y_C) \)
\( D’ = (x_D, -y_D) \)
\( C’ = (2, -4) \)
\( D’ = (1, -5) \)
Уравнение прямой, проходящей через две точки \( (x_1, y_1) \) и \( (x_2, y_2) \), имеет вид:
\( \frac{y — y_1}{y_2 — y_1} = \frac{x — x_1}{x_2 — x_1} \)
Подставляем координаты точек C’ и D’:
\( \frac{y — (-4)}{-5 — (-4)} = \frac{x — 2}{1 — 2} \)
\( \frac{y + 4}{-5 + 4} = \frac{x — 2}{-1} \)
\( \frac{y + 4}{-1} = \frac{x — 2}{-1} \)
Умножаем обе части на -1:
\( y + 4 = x — 2 \)
\( y = x — 2 — 4 \)
\( y = x — 6 \)

Ответ: \( y = x — 6 \)

б)
Пусть точка E имеет координаты \( (x_E, y_E) \) и точка F имеет координаты \( (x_F, y_F) \).
\( E = (-1, 4) \)
\( F = (2, -2) \)
Прямая, симметричная прямой EF относительно оси ординат, будет проходить через точки E» и F», где координаты этих точек являются отражением E и F относительно оси ординат.
Для отражения относительно оси ординат, координата y остается прежней, а координата x меняет знак.
\( E» = (-x_E, y_E) \)
\( F» = (-x_F, y_F) \)
\( E» = (-(-1), 4) = (1, 4) \)
\( F» = (-2, -2) \)
Используем уравнение прямой, проходящей через две точки \( (x_1, y_1) \) и \( (x_2, y_2) \):
\( \frac{y — y_1}{y_2 — y_1} = \frac{x — x_1}{x_2 — x_1} \)
Подставляем координаты точек E» и F»:
\( \frac{y — 4}{-2 — 4} = \frac{x — 1}{-2 — 1} \)
\( \frac{y — 4}{-6} = \frac{x — 1}{-3} \)
Умножаем обе части на -6:
\( y — 4 = \frac{-6}{-3}(x — 1) \)
\( y — 4 = 2(x — 1) \)
\( y — 4 = 2x — 2 \)
\( y = 2x — 2 + 4 \)
\( y = 2x + 2 \)

Ответ: \( y = 2x + 2 \)