ГДЗ по Алгебре 7 Класс Номер 10.8 Мордкович — Подробные Ответы

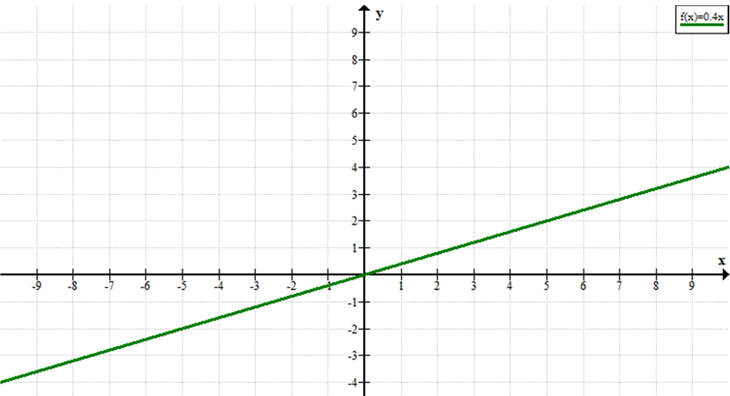
Постройте график линейной функции у = 0,4х. Найдите по графику: а) значение у, соответствующее значению х, равному 0; 5; 10; -5; б) значение х, которому соответствует значение у, равное 0; 2; 4; -2; в) решения неравенства 0,4x > 0; г) решения неравенства -2 < = 0,4x < = 0.

\( y = 0.4x \)

\( x = 0 \)

\( y = 0.4 \cdot 0 = 0 \)

\( x = 5 \)

\( y = 0.4 \cdot 5 = 2 \)

\( x = 10 \)

\( y = 0.4 \cdot 10 = 4 \)

\( x = -5 \)

\( y = 0.4 \cdot (-5) = -2 \)

б)
\( y = 0 \)

\( 0 = 0.4x \)

\( x = 0 \)

\( y = 2 \)

\( 2 = 0.4x \)

\( x = \frac{2}{0.4} = 5 \)

\( y = 4 \)

\( 4 = 0.4x \)

\( x = \frac{4}{0.4} = 10 \)

\( y = -2 \)

\( -2 = 0.4x \)

\( x = \frac{-2}{0.4} = -5 \)

в)
\( 0.4x > 0 \)

\( x > 0 \)

г)
\( -2 \le 0.4x \le 0 \)

\( \frac{-2}{0.4} \le x \le \frac{0}{0.4} \)

\( -5 \le x \le 0 \)

Условие:
Построить график \(y = 0,4x\) и найти значения \(y\) при \(x = 0, 5, 10, -5\), значения \(x\)
при \(y = 0, 2, 4, -2\), решения неравенств \(0,4x > 0\) и \(-2 \le 0,4x \le 0\).

Решение:
Для построения графика нужны две точки:
\(x_1 = 0, y_1 = 0,4 \cdot 0 = 0\)
— первая точка
\(x_2 = 5, y_2 = 0,4 \cdot 5 = 2\)
— вторая точка

а) Значения \(y\) при заданных \(x\):
\(x = 0, y = 0,4 \cdot 0 = 0\)

\(x = 5, y = 0,4 \cdot 5 = 2\)

\(x = 10, y = 0,4 \cdot 10 = 4\)

\(x = -5, y = 0,4 \cdot (-5) = -2\)

б) Значения \(x\) при заданных \(y\):
\(y = 0, x = 0 / 0,4 = 0\)

\(y = 2, x = 2 / 0,4 = 5\)

\(y = 4, x = 4 / 0,4 = 10\)

\(y = -2, x = -2 / 0,4 = -5\)

в) Решение неравенства \(0,4x > 0\):
\(x > 0\)
— делим на 0,4

г) Решение неравенства \(-2 \le 0,4x \le 0\):
\(-2 \le 0,4x\) и \(0,4x \le 0\)
— двойное неравенство
\(-5 \le x\) и \(x \le 0\)
— делим на 0,4
\(-5 \le x \le 0\)
— итоговое решение

Ответы:

а)
\(y(0) = 0\), \(y(5) = 2\), \(y(10) = 4\), \(y(-5) = -2\)

б)
\(x(0) = 0\), \(x(2) = 5\), \(x(4) = 10\), \(x(-2) = -5\)

в)
\(x > 0\)

г)
\(-5 \le x \le 0\)