ГДЗ по Алгебре 7 Класс Номер 13.12 Мордкович — Подробные Ответы

а) система 2x+\(y=1, 2x+y=3\); б)система \(y=\frac{2x}{5}-1, 4x-10y=10\); в)система \(y=\frac{-1x}{3}+2, x+3y=3\); г)система x-3\(y=2, 2x-36y=4. \)

а)
\(
\begin{cases}
2x+y=1 \\
2x+y=3
\end{cases}
\)
\(
y = 1 — 2x
\)
\(
2x + (1 — 2x) = 3
\)
\(
1 = 3
\)

б)
\(
\begin{cases}
y=\frac{2x}{5}-1 \\
4x-10y=10
\end{cases}
\)
\(
4x — 10(\frac{2x}{5}-1) = 10
\)
\(
4x — 4x + 10 = 10
\)
\(
10 = 10
\)

в)
\(
\begin{cases}
y=-\frac{1}{3}x+2 \\
x+3y=3
\end{cases}
\)
\(
x + 3(-\frac{1}{3}x+2) = 3
\)
\(
x — x + 6 = 3
\)
\(
6 = 3
\)

г)
\(
\begin{cases}
x-3y=2 \\
2x-6y=4
\end{cases}
\)
\(
x = 3y + 2
\)
\(
2(3y + 2) — 6y = 4
\)
\(
6y + 4 — 6y = 4
\)
\(
4 = 4
\)

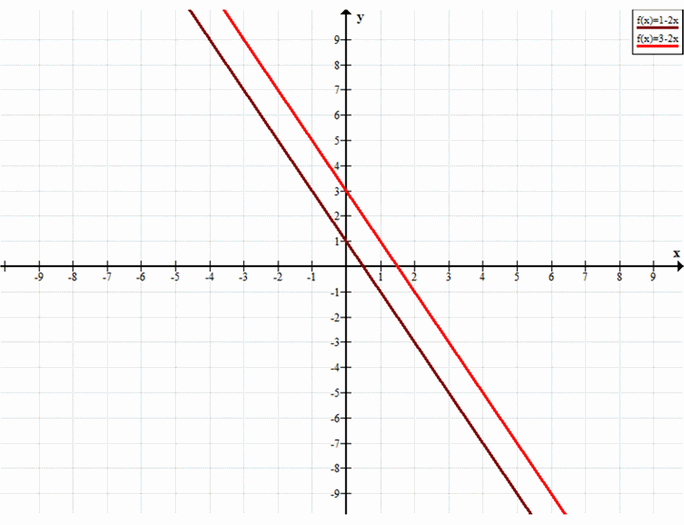
а) Система \(2x+y=1, 2x+y=3\)

\(2x + y = 1\)
— первое уравнение
\(2x + y = 3\)
— второе уравнение

Выражения в левой части равны, а правые части разные, значит система не имеет решений.

Решений нет.

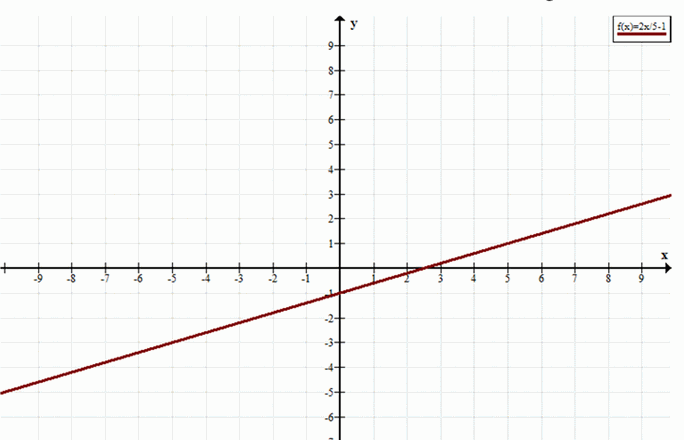
б) Система \(y=\frac{2x}{5}-1, 4x-10y=10\)

\(y = \frac{2x}{5} — 1\)
— первое уравнение
\(4x — 10y = 10\)
— второе уравнение

Подставим первое уравнение во второе:
\(4x — 10(\frac{2x}{5} — 1) = 10\)
— подстановка
\(4x — 4x + 10 = 10\)
— раскрываем скобки
\(10 = 10\)
— получили верное равенство

Система имеет бесконечно много решений.

Бесконечно много решений.

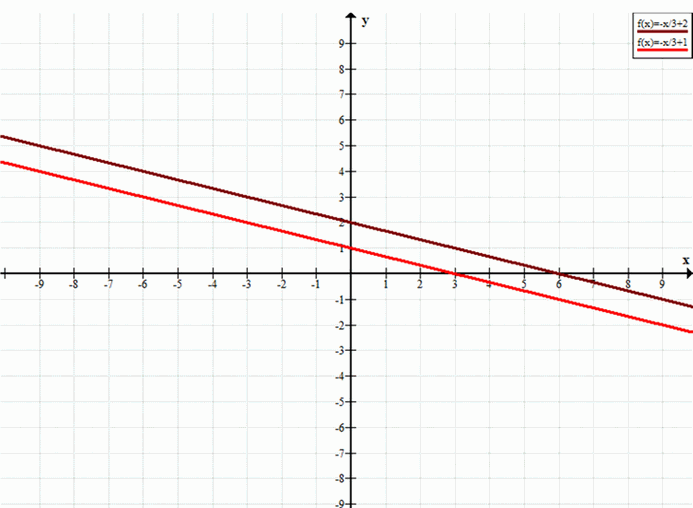
в) Система \(y=-\frac{x}{3}+2, x+3y=3\)

\(y = -\frac{x}{3} + 2\)
— первое уравнение
\(x + 3y = 3\)
— второе уравнение

Подставим первое уравнение во второе:
\(x + 3(-\frac{x}{3} + 2) = 3\)
— подстановка
\(x — x + 6 = 3\)
— раскрываем скобки
\(6 = 3\)
— получили неверное равенство

Система не имеет решений.

Решений нет.

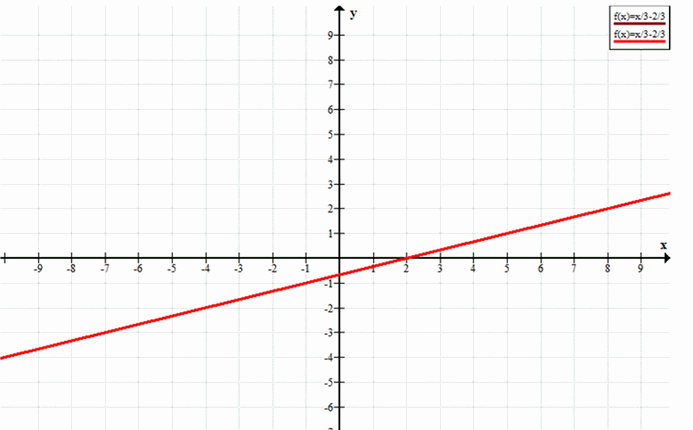
г) Система \(x-3y=2, 2x-6y=4\)

\(x — 3y = 2\)
— первое уравнение
\(2x — 6y = 4\)
— второе уравнение

Умножим первое уравнение на 2:
\(2(x — 3y) = 2 \cdot 2\)
— умножение
\(2x — 6y = 4\)
— получили второе уравнение

Система имеет бесконечно много решений.

Бесконечно много решений.