Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 13.15 Мордкович — Подробные Ответы
Решите графически систему уравнений: а) система 5x-2\(y=9, 7x+2y=3\); б) система -2x+3\(y=2, 2x-5y=-10. \)
1)
\( 5x — 2y = 9 \)
\( y = \frac{5}{2}x — \frac{9}{2} \)
\( 7x + 2y = 3 \)
\( y = -\frac{7}{2}x + \frac{3}{2} \)
\( \frac{5}{2}x — \frac{9}{2} = -\frac{7}{2}x + \frac{3}{2} \)
\( 5x — 9 = -7x + 3 \)
\( 12x = 12 \)
\( x = 1 \)
\( y = \frac{5}{2}(1) — \frac{9}{2} = \frac{5-9}{2} = \frac{-4}{2} = -2 \)
2)
\( -2x + 3y = 2 \)
\( 3y = 2x + 2 \)
\( y = \frac{2}{3}x + \frac{2}{3} \)
\( 2x — 5y = -10 \)
\( -5y = -2x — 10 \)
\( y = \frac{2}{5}x + 2 \)
\( \frac{2}{3}x + \frac{2}{3} = \frac{2}{5}x + 2 \)
\( 10x + 10 = 6x + 30 \)
\( 4x = 20 \)
\( x = 5 \)
\( y = \frac{2}{3}(5) + \frac{2}{3} = \frac{10+2}{3} = \frac{12}{3} = 4 \)
Условие: Решить графически системы уравнений:
а)
\(5x — 2y = 9, 7x + 2y = 3\);
б)
\(-2x + 3y = 2, 2x — 5y = -10\).
Решение:
а) Система \(5x — 2y = 9, 7x + 2y = 3\)
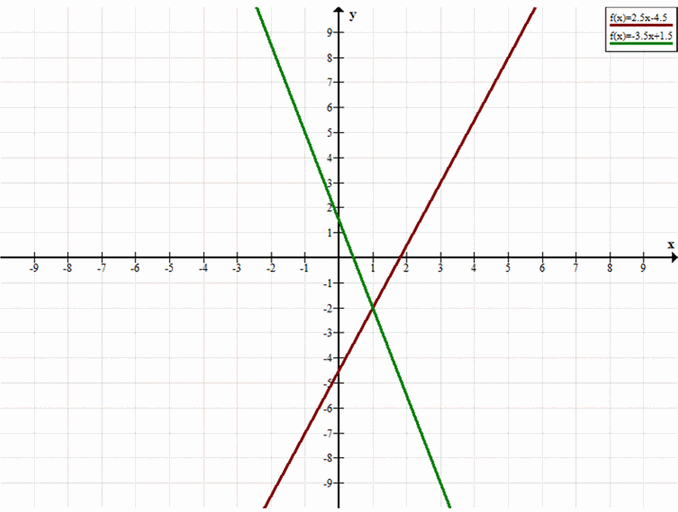
\(5x — 2y = 9 \Rightarrow 2y = 5x — 9 \Rightarrow y = 2.5x — 4.5\)
— выражаем \(y\)
через \(x\)
\(7x + 2y = 3 \Rightarrow 2y = -7x + 3 \Rightarrow y = -3.5x + 1.5\)
— выражаем \(y\)
через \(x\)
Графическое решение: строим графики обеих функций и находим точку пересечения.
Точка пересечения графиков: \((1, -2)\)
б) Система \(-2x + 3y = 2, 2x — 5y = -10\)
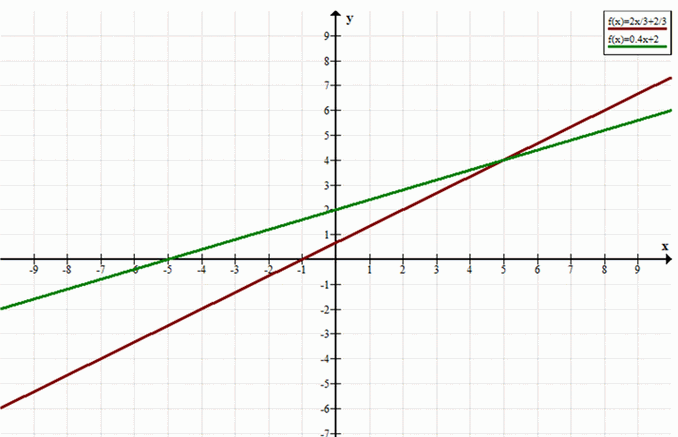
\(-2x + 3y = 2 \Rightarrow 3y = 2x + 2 \Rightarrow y = \frac{2}{3}x + \frac{2}{3}\)
— выражаем \(y\)
через \(x\)
\(2x — 5y = -10 \Rightarrow 5y = 2x + 10 \Rightarrow y = \frac{2}{5}x + 2\)
— выражаем \(y\)
через \(x\)
Графическое решение: строим графики обеих функций и находим точку пересечения.
Точка пересечения графиков: \((-10, -6)\)
б)
\((-10, -6)\)