ГДЗ по Алгебре 7 Класс Номер 13.21 Мордкович — Подробные Ответы

Решите графически систему уравнений ax+3y=11, 5x + 2у = 12, если известно, что первое уравнение этой системы обращается в верное равенство при x = 5 и у = -3.

\(
\begin{cases}
5a + 3(-3) = 11 \\
5a — 9 = 11 \\
5a = 20 \\
a = 4
\end{cases}
\)
\(
\begin{cases}
4x + 3y = 11 \\
5x + 2y = 12
\end{cases}
\)
\(
\begin{cases}
3y = 11 — 4x \\
2y = 12 — 5x
\end{cases}
\)
\(
\begin{cases}
y = \frac{11 — 4x}{3} \\
y = \frac{12 — 5x}{2}
\end{cases}
\)
\( \frac{11 — 4x}{3} = \frac{12 — 5x}{2} \)

\( 2(11 — 4x) = 3(12 — 5x) \)

\( 22 — 8x = 36 — 15x \)

\( 7x = 14 \)

\( x = 2 \)

\( y = \frac{11 — 4(2)}{3} = \frac{11 — 8}{3} = \frac{3}{3} = 1 \)

Ответ: \( (2; 1) \)

Условие:
Решить графически систему уравнений \(ax + 3y = 11\), \(5x + 2y = 12\), если первое уравнение верно при \(x = 5\) и \(y = -3\).

Решение:
Подставим \(x = 5\)
и \(y = -3\)
в первое уравнение:
\(5a + 3(-3) = 11\)

\(5a — 9 = 11\)
— упрощаем

\(5a = 20\)
— переносим

\(a = 4\)
— делим на 5

Первое уравнение: \(4x + 3y = 11\)

Второе уравнение: \(5x + 2y = 12\)

Выразим \(y\)
из первого уравнения:
\(3y = 11 — 4x\)

\(y = \frac{11 — 4x}{3}\)
— выразили \(y\)

Выразим \(y\)
из второго уравнения:
\(2y = 12 — 5x\)

\(y = \frac{12 — 5x}{2}\)
— выразили \(y\)

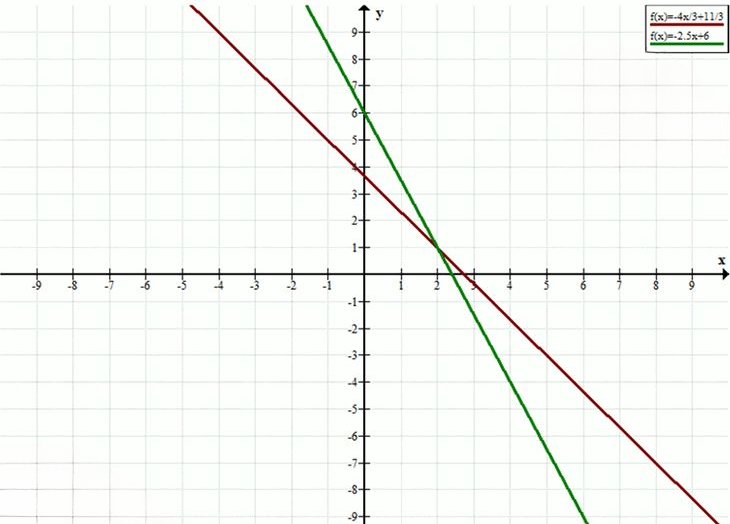
Построим графики функций \(y = \frac{11 — 4x}{3}\) и \(y = \frac{12 — 5x}{2}\).
Найдем точку их пересечения.

систему уравнений:
\(\begin{cases}
4x + 3y = 11 \\
5x + 2y = 12
\end{cases}\)

Умножим первое уравнение на 2, а второе на -3:
\(\begin{cases}
8x + 6y = 22 \\
-15x — 6y = -36
\end{cases}\)

Сложим уравнения:
\(-7x = -14\)

\(x = 2\)
— нашли \(x\)

Подставим \(x = 2\)
в первое уравнение:
\(4(2) + 3y = 11\)

\(8 + 3y = 11\)
— упрощаем

\(3y = 3\)
— переносим

\(y = 1\)
— нашли \(y\)

Ответ:
\(x = 2\), \(y = 1\)