Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 23.3 Мордкович — Подробные Ответы
Во всех школах микрорайона была проведена проверочная работа по теме «Степень с натуральным показателем и её свойства». Работу по болезни не писали 20 семиклассников.
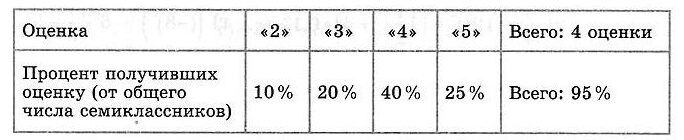
Вот итоги работы:
a) Какой процент составляют школьники, пропустившие эту контрольную?
б) Найдите общее количество семиклассников микрорайона.
в) Сколько школьников составляют 1% от общего числа семиклассников в этих школах?
г) Сколько всего семиклассников получили «4» или «5»?
\[
а)\ 100\% — 95\% = 5\%\ \text{(пропустили)}
\]
\[
б)\ 20\ \text{чел.} \rightarrow 5\%
\]
\[
\frac{20}{0{,}05} = \frac{20}{0{,}05} = 400\ \text{чел.}
\]
\[
в)\ 1\%\ \text{от}\ 400 = 4\ \text{чел.}
\]
\[
г)\ «4»\ \text{или}\ «5» = 40\% + 25\% = 65\%
\]
\[
65\%\ \text{от}\ 400 = 0{,}65 \cdot 400 = 260\ \text{чел.}
\]
Дано:
Проценты учащихся, получивших оценки:
«2» — 10 %,
«3» — 20 %,
«4» — 40 %,
«5» — 25 %.
В сумме эти проценты дают 95 %, то есть 95 % всех семиклассников писали контрольную работу.
а) Какой процент учащихся пропустил контрольную?
Общее количество учащихся принимается за 100 %.
Если 95 % писали контрольную, то остальные не писали.
\[
100\% — 95\% = 5\%
\]
Таким образом, 5 % учащихся пропустили контрольную.
б) Известно, что 20 человек пропустили контрольную. Сколько всего семиклассников?
Из пункта (а) известно, что 20 человек составляют 5 % от общего числа учащихся.
Обозначим общее число учащихся за \( N \). Тогда:
\[
0{,}05 \cdot N = 20
\]
Решим это уравнение:
\[
N = \frac{20}{0{,}05}
\]
\[
N = \frac{20 \cdot 100}{5}
\]
\[
N = \frac{2000}{5}
\]
\[
N = 400
\]
Итак, всего 400 семиклассников.
в) Сколько человек составляет 1 % от общего числа учащихся?
Общее число учащихся: 400.
1 % от 400:
\[
0{,}01 \cdot 400 = 4
\]
Значит, 1 % соответствует 4 учащимся.
г) Сколько учащихся получили оценку «4» или «5»?
Из таблицы:
«4» получили 40 %,
«5» получили 25 %.
Суммарный процент:
\[
40\% + 25\% = 65\%
\]
Теперь найдём, сколько это человек от общего числа \( N = 400 \):
\[
0{,}65 \cdot 400 = 260
\]
Альтернативно, используя результат пункта (в):
1 % = 4 человека, следовательно:
\[
65 \cdot 4 = 260
\]
Таким образом, 260 учащихся получили оценку «4» или «5».
Ответы:
а) \( 5\% \)
б) \( 400 \) человек
в) \( 4 \) человека
г) \( 260 \) человек