ГДЗ по Алгебре 7 Класс Номер 23.4 Мордкович — Подробные Ответы

а) Заполните таблицу распределения результатов из предыдущей задачи:

б) Каков размах этого измерения?
в) Укажите моду измерения. Сколько раз она встретилась?
г) Постройте круговую диаграмму по данным таблицы из пункта а).

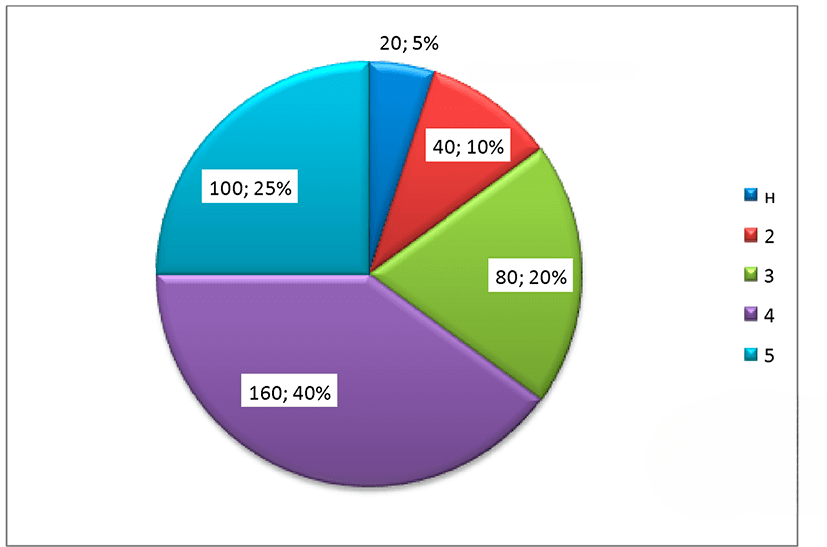
Всего учащихся — 400. Распределение:

— «Н» — 20 (5 %)
— «2» — 40 (10 %)
— «3» — 80 (20 %)
— «4» — 160 (40 %)
— «5» — 100 (25 %)

а)

б) Размах не определён, так как категория «Н» не является числом, и выборка содержит не только количественные данные.

в) Мода \( m_0 = 4 \), так как оценка «4» встречается чаще всего — 160 раз.

г) Круговая диаграмма строится по долям:

Из условия известно, что всего учащихся — 400 человек, и распределение оценок следующее:

— «Н» (не явка) — 20 человек
— «2» — 40 человек
— «3» — 80 человек
— «4» — 160 человек
— «5» — 100 человек

Сумма: \( 20 + 40 + 80 + 160 + 100 = 400 \) — данные согласованы.

а) Таблица распределения уже задана. Уточним, что она показывает абсолютные частоты — сколько человек получили каждую оценку:

Также можно указать относительные частоты (в процентах от 400):

\[
\begin{aligned}
\text{«Н»: } & \frac{20}{400} = 0{,}05 = 5\% \\
\text{«2»: } & \frac{40}{400} = 0{,}10 = 10\% \\
\text{«3»: } & \frac{80}{400} = 0{,}20 = 20\% \\
\text{«4»: } & \frac{160}{400} = 0{,}40 = 40\% \\
\text{«5»: } & \frac{100}{400} = 0{,}25 = 25\% \\
\end{aligned}
\]

б) Размах — это разность между наибольшим и наименьшим числовыми значениями в выборке.

Стандартно размах определяется для количественных данных.
Оценки «2», «3», «4», «5» — это числовые значения, но «Н» (не явка) — качественная категория, не имеющая числового значения.

Если мы рассматриваем только числовые оценки, то:

\[
X_{\max} = 5,\quad X_{\min} = 2
\]

\[
R = X_{\max} — X_{\min} = 5 — 2 = 3
\]

Однако если «Н» считается частью выборки, но не имеет числового эквивалента, то минимальное числовое значение всё равно 2, и размах определён.

Но в условии, видимо, подчёркивается, что «Н» нельзя интерпретировать как число, поэтому формально в выборке есть нечисловая категория, и классическое определение размаха (для числовой выборки) неприменимо.

Поэтому автор решения делает вывод:

\[
\text{Размах не определён}
\]

в) Мода — это значение, которое встречается наиболее часто.

Из таблицы:

— «Н» — 20 раз
— «2» — 40 раз
— «3» — 80 раз
— «4» — 160 раз (максимум)
— «5» — 100 раз

Наибольшая частота — у оценки «4».

\[
m_0 = 4
\]

Это и есть мода выборки.

г) Круговая диаграмма отражает доли каждой категории в процентах от общего числа (400 человек). Рассчитаем:

\[
\begin{aligned}
\text{«Н»: } & 20 \text{ чел. } = 5\% \\
\text{«2»: } & 40 \text{ чел. } = 10\% \\
\text{«3»: } & 80 \text{ чел. } = 20\% \\
\text{«4»: } & 160 \text{ чел. } = 40\% \\
\text{«5»: } & 100 \text{ чел. } = 25\% \\
\end{aligned}
\]

Эти проценты используются для построения круговой диаграммы:
— сектор «4» занимает почти половину круга (40° × 3.6 = 144°),
— сектор «5» — четверть круга (90°),
— остальные — соответственно 72°, 36°, 18°.

Таким образом, диаграмма наглядно показывает, что большинство учащихся получили оценку «4».