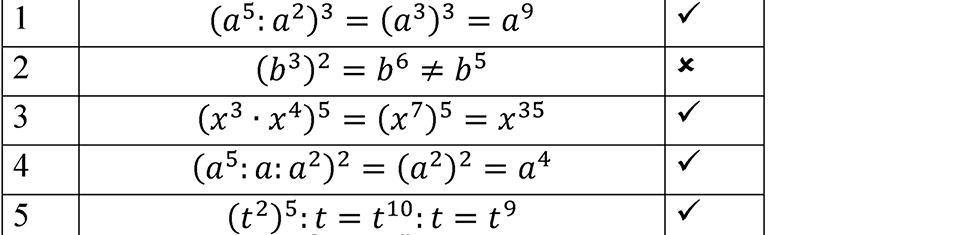Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 23.5 Мордкович — Подробные Ответы
Среди следующих равенств есть верные, но могут быть и неверные:
\[(a^5 : a^2)^3 = a^9, \quad (b^3)^2 = b^5, \quad (x^3 : x^4)^5 = x^{35},\]
\[(a^5 : a : a^2)^2 = a^4, \quad (t^2)^5 : t = t^9.\]
На карточке № 1 записывают одно из равенств, а на карточке № 2 — одно из оставшихся равенств.
a) Сколько существует способов такого выбора двух равенств?
б) В скольких случаях на обеих карточках будут верные равенства?
в) В скольких случаях на обеих карточках будут неверные равенства?
г) В скольких случаях основания степеней на обеих карточках совпадут между собой?
(а) На первую карточку можно записать 5 равенств, на вторую — 4 оставшихся. Всего 5 · 4 = 20 способов.
(б) На первую карточку можно записать 4 верных равенства, на вторую — 3 оставшихся. Всего 4 · 3 = 12 способов.
(в) Неверных равенств только одно. На обеих карточках не может быть неверных равенств — 0 способов.
(г) Основания степеней совпадают в 2 равенствах. На первую карточку можно записать 2 таких равенства, на вторую — 1 оставшееся. Всего 2 · 1 = 2 способа.
Равенство 1:
\[
(a^5 : a^2)^3 = (a^3)^3 = a^9
\]
\[
a^5 : a^2 = a^{5 — 2} = a^3
\]
\[
(a^3)^3 = a^{3 \cdot 3} = a^9
\]
Равенство верно.
Равенство 2:
\[
(b^3)^2 = b^6 \neq b^5
\]
\[
(b^3)^2 = b^{3 \cdot 2} = b^6
\]
Поскольку \( b^6 \neq b^5 \) (при \( b \neq 0, 1 \)), равенство неверно.
Равенство 3:
\[
(x^3 \cdot x^4)^5 = (x^7)^5 = x^{35}
\]
\[
x^3 \cdot x^4 = x^{3 + 4} = x^7
\]
\[
(x^7)^5 = x^{7 \cdot 5} = x^{35}
\]
Равенство верно.
Равенство 4:
\[
(a^5 : a : a^2)^2 = (a^2)^2 = a^4
\]
\[
a^5 : a = a^{5 — 1} = a^4
\]
\[
a^4 : a^2 = a^{4 — 2} = a^2
\]
\[
(a^2)^2 = a^{2 \cdot 2} = a^4
\]
Равенство верно.
Равенство 5:
\[
(t^2)^5 : t = t^{10} : t = t^9
\]
\[
(t^2)^5 = t^{2 \cdot 5} = t^{10}
\]
\[
t^{10} : t = t^{10 — 1} = t^9
\]
Равенство верно.
Итак, из пяти равенств четыре верны (1, 3, 4, 5) и одно неверно (2).
Теперь ответим на вопросы.
(а) Сколькими способами можно выбрать две карточки (порядок важен), на которых записаны любые два разных равенства из пяти?
Выбираем первую карточку: 5 вариантов.
Выбираем вторую карточку: остаётся 4 оставшихся равенства.
Порядок важен, поэтому умножаем:
\[
5 \cdot 4 = 20
\]
Ответ: \( 20 \)
(б) Сколькими способами можно выбрать две карточки с верными равенствами?
Верных равенств — 4.
Первая карточка: 4 варианта.
Вторая карточка: 3 оставшихся верных равенства.
\[
4 \cdot 3 = 12
\]
Ответ: \( 12 \)
(в) Сколькими способами можно выбрать две карточки, обе с неверными равенствами?
Неверных равенств — только одно (равенство 2).
Невозможно выбрать два разных неверных равенства.
\[
0 \text{ способов}
\]
Ответ: \( 0 \)
(г) Сколькими способами можно выбрать две карточки, в которых основания степеней совпадают?
Рассмотрим каждое равенство:
1. основание \( a \)
2. основание \( b \)
3. основание \( x \)
4. основание \( a \)
5. основание \( t \)
Только равенства 1 и 4 имеют одинаковое основание \( a \).
Других совпадений нет.
Таким образом, таких равенств — 2.
Выбираем первую карточку: 2 варианта.
Выбираем вторую: остаётся 1.
\[
2 \cdot 1 = 2
\]
Ответ: \( 2 \)
Ответ:
а) \( 20 \)
б) \( 12 \)
в) \( 0 \)
г) \( 2 \)