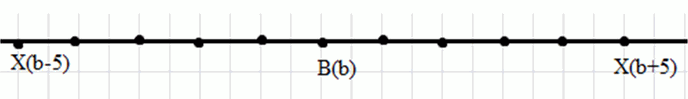Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 3.6 Мордкович — Подробные Ответы
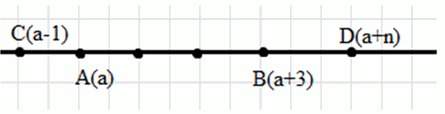
а) На координатной прямой дана точка А(а) и точки В(а + 3), С(а — 1), D(a + n); б) на координатной прямой даны точка В(b) и точка X, удалённая от точки В на расстояние, равное 5; в) расстояние от точки O(0) до точки Т равно m единичных отрезков; г) расстояние от точки А(а) до точки В равно r единичных отрезков.
а)
\( B(a+3) \)
\( C(a-1) \)
\( D(a+n) \)
б)
\( X_1 = b — 5 \)
\( X_2 = b + 5 \)
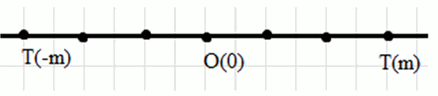
в)
\( T_1 = -m \)
\( T_2 = m \)
г)
\( |a — b| = r \)
\( a — b = r \) или \( a — b = -r \)
\( b = a — r \) или \( b = a + r \)
а) Координаты точек:
\(A(a)\)
— дана
\(B(a + 3)\)
— дана
\(C(a — 1)\)
— дана
\(D(a + n)\)
— дана
б) Координаты точки X:
\(B(b)\)
— дана
\(X_1 = b + 5\)
— вправо на 5
\(X_2 = b — 5\)
— влево на 5
в) Координаты точки T:
\(O(0)\)
— дана
\(T_1 = 0 + m = m\)
— вправо на m
\(T_2 = 0 — m = -m\)
— влево на m
г) Расстояние между точками A и B:
\(A(a)\)
— дана
\(B_1 = a + r\)
— вправо на r
\(B_2 = a — r\)
— влево на r
а)
\(A(a), B(a+3), C(a-1), D(a+n)\)
б)
\(X_1(b+5), X_2(b-5)\)
в)
\(T_1(m), T_2(-m)\)
г)
\(B_1(a+r), B_2(a-r)\)